Post ini adalah materi lanjutan dari materi-materi bilangan kompleks sebelumnya. Karena ini adalah post berantai, diharapkan agar pembaca memahami 100% post sebelumnya sbb:
(i) Mengenal Bilangan Kompleks
(ii) Dalil De Moivre
(iii) Persamaan Euler
(iv) Review
Di post ini, kita akan melanjutkan materi mengenai bilangan kompleks, yang merupakan pengembangan dari materi-materi di atas... Guampang lowh.. ^^
(i) Mengenal Bilangan Kompleks
(ii) Dalil De Moivre
(iii) Persamaan Euler
(iv) Review
Di post ini, kita akan melanjutkan materi mengenai bilangan kompleks, yang merupakan pengembangan dari materi-materi di atas... Guampang lowh.. ^^
=========================================================================
FUNGSI KOMPLEKS
LOGARITMA BASIS NATURAL
LOGARITMA BASIS NATURAL
Masih ingatkah dengan persamaan euler?
Kalau belom, silakan baca post sebelumnya (lihat di atas)...
Kalau sudah, silakan tulis persamaan itu di secarik kertas...
Ikuti langkah di bawah..
Pers euler adalah sebagai berikut.



 (memiliki banyak nilai)
(memiliki banyak nilai)

 ... (i)
... (i)Selanjutnya, kita ingin menentukan formula dari
 . Kita ubah z ke dalam polar.
. Kita ubah z ke dalam polar.

 , maka:
, maka:
 .
.Contoh:
| 1. | Ubah menjadi bentuk koordinat dan tentukanlah harga dasarnya: a)  b)  Jawab: a)  = =  = =  ____________untuk ____________untuk  Harga dasarnya didapat dengan mensubstitusikan n= 0, maka:  b)  ____________untuk ____________untuk  Harga dasarnya didapat dengan mensubstitusikan n= 0, maka:  |
=========================================================================
PEMANGKATAN KOMPLEKS
Diberikan sebuah formula pemangkatan kompleks sebagai berikut:

berlaku untuk z dan w semua bilangan kompleks.

Kita ln-kan kedua ruas:


Kemudian jadikan kedua ruas sebagai pangkat dari e.


Dengan demikian:

(Terbukti)
Contoh:
| 2. | Tentukanlah nilai dasar dari: a.  b.  Jawab: a)  = =  _____________=  _____________=  _____________=  _____________=  _____________=  Note: Soal di atas ditujukan agar kalian memahami pengerjaan pemangkatan kompleks. Pada kenyataannya, tidak ada masalah yang sekompleks itu.. :).. b.  = = 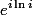 = =  = =  = =  = 0,207879576 = 0,207879576Note: jawaban di atas silakan di cek di google, dengan mengetikkan "i^i".. Jawaban ini merupakan jawaban spesial di mana suatu kompleks yang dipangkatkan kompleks akan menghasilkan bilangan Real.. |
=========================================================================
Note: Materi ini adalah materi universitasku semester 4 hingga pertemuan ke-6.
Silakan bertanya jika ada yang ingin ditanyakan.. ^^

http://hendrydext.blogspot.com/
ReplyDeletemakasih atas blog na...
ReplyDeletesaya akan coba pelajari bilangan kompleks yg ad d blog ini...
mau donk sambungannya..tentang limit fungsi kompleks..
ReplyDeletemas
ReplyDeletelanjutannya mana??????????????????????
jgn ;ama2 y kami dah mau ujian ni