1. Ada berapa banyak digit dari  setelah diuraikan?
setelah diuraikan?
2. Tentukan digit terakhir dari
3. Tentukan digit ke-99 di belakang koma pada .
.
Hint: **Yang paling mudah adalah nomor 2, yaitu modulo 10 biasa.. Nomor 1 dan 3 diselesaikan dengan cara yang sedikit kreatif, yaitu dengan cara membandingkannya dengan bilangan lain yang lebih besar atau lebih kecil.. Very challenging... ^^**
 setelah diuraikan?
setelah diuraikan?2. Tentukan digit terakhir dari

3. Tentukan digit ke-99 di belakang koma pada
 .
.Hint: **Yang paling mudah adalah nomor 2, yaitu modulo 10 biasa.. Nomor 1 dan 3 diselesaikan dengan cara yang sedikit kreatif, yaitu dengan cara membandingkannya dengan bilangan lain yang lebih besar atau lebih kecil.. Very challenging... ^^**
=========================================================================
JAWABAN
| 1. | Bilangan  akan lebih mudah dibentuk menjadi akan lebih mudah dibentuk menjadi  . Kemudian, kita mencoba melihat angka-angka lain yang lebih besar dan lebih kecil dari angka tersebut untuk menaksir jumlah digit dari . Kemudian, kita mencoba melihat angka-angka lain yang lebih besar dan lebih kecil dari angka tersebut untuk menaksir jumlah digit dari  . .Perhatikan bahwa:   memiliki 31 digit, maka memiliki 31 digit, maka  sedikitnya memiliki 31 digit. sedikitnya memiliki 31 digit.Kemudian perhatikan bahwa:     Mengingat bahwa  , sehingga pertaksamaan ini berlaku: , sehingga pertaksamaan ini berlaku:       harus lebih kecil dari 32.. harus lebih kecil dari 32..Namun, syarat di awal mengharuskan digit dari  setidaknya 31 digit. setidaknya 31 digit.Kesimpulannya,  memiliki 31 digit. memiliki 31 digit. |
| 2. | Seperti bahasan modulo yang pernah kita bahas sebelumnya di post INI. Maka, kita menggunakan cara yang serupa. Untuk mencari digit terakhir dari  , kita gunakan modulo 10. Namun, masalahnya sekarang adalah pangkatnya yang dipangkatkan. Maka, kita sederhanakan pangkatnya terlebih dahulu dengan modulo lagi. Di sini, kita gunakan modulo 4. , kita gunakan modulo 10. Namun, masalahnya sekarang adalah pangkatnya yang dipangkatkan. Maka, kita sederhanakan pangkatnya terlebih dahulu dengan modulo lagi. Di sini, kita gunakan modulo 4. . . menghasilkan sisa 3 jika dibagi dengan 4, maka menghasilkan sisa 3 jika dibagi dengan 4, maka  dapat dibentuk sbb: dapat dibentuk sbb: . .Maka:  ____________=  ____________=  ____________= 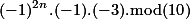 ____________=  ____________= 3. Jadi, digit terakhirnya adalah 3. |
| 3. | Jika Jadi  diuraikan dengan teorema binomial, maka semua pangkat ganjil dari diuraikan dengan teorema binomial, maka semua pangkat ganjil dari  akan habis, sehingga hasilnya bilangan bulat. Perhatikan bahwa akan habis, sehingga hasilnya bilangan bulat. Perhatikan bahwa  pasti dimulai dengan 150 angka 0 di belakang koma, sehingga pasti dimulai dengan 150 angka 0 di belakang koma, sehingga  harus dimulai dengan 150 angka 9 di belakang koma, agar jumlahnya bulat. Maka digit ke-99 di belakang koma adalah 9. harus dimulai dengan 150 angka 9 di belakang koma, agar jumlahnya bulat. Maka digit ke-99 di belakang koma adalah 9. |

yang no1 31 digit ya?
ReplyDeletewkakakakak gak habis pikir aku.... wa cuman isa nemuin polanya tapi gak isa nemuin nilainya buat nomer2
ReplyDeletejangarrr....
ReplyDeletelog 2 = 0.30102995...
ReplyDeletelog 2^100 = 100 log 2 = 30.102...
30 < 30.102... < 31
log 10^30 < log 2^100 < log 10^31
10^30 < 2^100 < 10^31
maka jumlah digitnya pasti 31. (QED)