Tentunya, sebagian besar dari pembaca sudah mengenal istilah magic square.
Ingin mengenal lebih jauh tentang magic square. Silakan lihat post di bawah. :)
=======================================================================
Sejarah *Sangat Singkat* Magic Square:
Persegi ajaib sudah dikenal oleh matematikawan Cina sejak 650 Sebelum Masehi. Ada kemungkinan sudah dikenal oleh matematikawan Arab sejak abad ke-7.
Menurut literatur Cina, terdapat legenda bahwa dahulu kala terdapat bencana banjir. Raja besar Yu (禹) berusaha untuk menyalurkan air ke laut. Pada saat itu, terlihat kura-kura dengan pola aneh pada tempurung. Ini yang menjadi landasan untuk membuat suatu persegi 3x3 di mana setaip baris, kolom dan diagonalnya sama. Pola ini, dengan cara tertentu, juga digunakan oleh orang-orang dalam mengendalikan sungai.
Selanjutnya, magic square terus dipelajari dan dikembangkan di berbagai tempat.
Selengkapnya, silakan baca di http://en.wikipedia.org/wiki/Magic_square.
Beberapa istilah/kasus Magic Square yang menarik untuk diketahui:
Normal Magic Square
| adalah persegi yang dibentuk dengan menempatkan angka 1 hingga n2. dan tidak ada bilangan yang sama.
Contoh: magic square 3x3 yang diisi dengan angka 1 hingga 9.
Dalam pembahasan kita, jika dikatakan hanya "magic square", maka artinya kita membicarakan "normal magic square".
|
Semi Magic Square
| Semi Magic Square hanya mengharuskan angka pada baris dan kolom berjumlah sama, namun diagonal tidak perlu sama.
|
| Trivia Magic Square | Jika magic square berbentuk 1x1 atau semua angka pada petak diisi dengan angka yang sama semuanya, maka magic square itu adalah trivial. |
| Associative Magic Square | adalah normal magic square di mana petak di tengahnya adalah median dari bilangan-bilangan yang diisi.
Misalnya, untuk persegi 5x5 bagian tengahnya diisi dengan 13, maka disebut associative magic square.
|
Pan Magic Square
| Adalah normal magic square yang lebih ampuh, karena selain semua kolom dan barisnya sama, penjumlahan semua diagonalnya selalu sama. (diagonal ini melewati batas persegi).
Contoh:
Tidak ada pan magic square yang dapat dibentuk dari 3x3.
|
Concentric Magic Square
| Merupakan normal Magic Square nxn dengan n adalah ganjil dan n≥5 dan setiap persegi di dalamnya juga magic square.
Contoh:
Perhatikan bahwa persegi 3x3 di dalamnya juga adalah persegi ajaib dengan jumlah 39.
|
| Multiplicative Magic Square | Jika normal magic square menggunakan operasi penjumlahan, maka multiplicative magic square menggunakan operasi perkalian. Perkalian setiap baris, kolom, dan diagonalnya adalah sama.
Contoh:
 ____ |
Fakta-fakta singkat Magic Square:
| 1. | Suatu magic square 3x3 yang tidak harus normal (artinya angkanya bebas, tidak perlu urut), maka angka di bagian tengahnya selalu 1/3 dari jumlah total. Bisakah kalian membuktikannya?
Sebagai contoh:
Perhatikan bahwa 5 adalah 1/3 dari 15 (jumlah total per baris/kolom/diagonal).
Hint: Misalkan dari 9 kotak, asumsikan ada kotak yang bernilai a, b, dan c
|
| 2. | Suatu normal magic square
3x3 hanya dapat dibentuk dengan 1 cara (tidak termasuk rotasi, refleksi)
4x4 dalam 880 cara.
5x5 dalam 275305224 cara.
6x6 diperkirakan mencapai 1.7745×1019 cara.
|
Mengkontruksi Magic Square
Mengkontruksi magic square dapat dilakukan dengan komputer. Ada pula yang dilakukan secara matematis (perhitungan) manual menggunakan konsep modulo.
Di post ini, kita tidak akan menggunakan perhitungan matematis, tapi menggunakan metode-metode yang lebih mudah dipahami dan *klasik*, yaitu Siamese, Conway's LUX, Doubly Even (Lozenge) Method, dan Strachey Method (metode yang paling ribet).
Semua metode itu akan dibahas di bawah...
Siamese Method / de la Loubère Method
Kemungkinan besar, kalian sudah pernah mendengar cara meng"konstruksi" magic square siamese ini. (Dan, ini mungkin sudah sangat basi sekali kalau dijelaskan lagi)..
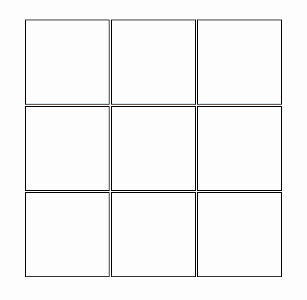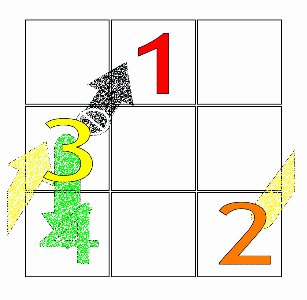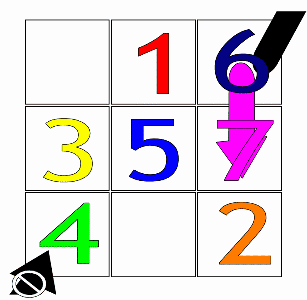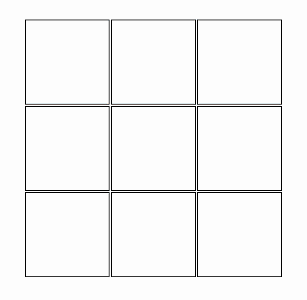
Lihat ilustrasi di bawah.
Metode di atas disebut juga sebagai metode Siamese. atau juga sering disebut dengan metode de la Loubère (bacanya susah..). Ingat: Metode Siamese hanya berlaku bagi persegi ganjil , misalnya 3x3, 5x5, 7x7.
Langkah-langkah metode Siamese secara general adalah sebagai berikut:
1. Dimulai dari angka 1. Tempatkan di baris teratas, tepat di petak tengah..
2. Kita bergerak ke kanan atas... Jika posisinya sudah berada di paling atas, maka pindah ke paling bawah. Jika posisinya sudah berada di paling kanan, maka pindah ke paling kiri. Kalau sudah ada petak yang terisi, pindah ke petak di bawahnya.. Ulangi langkah ini sampai semua petak terisi.
Perhatikan ilustrasi animasi di atas. Pasti jelas deh. Sebagai latihan, coba kalian buat persegi ajaib untuk 5x5 dengan metode Siamese ini. Yang sudah tahu boleh lanjut, tapi bagi yang pertama kali denger cara ini, kalian wajib dan kudu latihan.. weks. Masak maunya disuapin mlolo. ;p.
Berikut adalah persegi ajaib 5x5 dengan Metode Siamese (silakan dicocokan dengan jawabanmu)
Oit. Bagaimana kalau angka 1-nya ingin diletakkan di tempat yang berbeda? Jawabnya, ya!! Bisa. Tapi, aturannya bisa sedikit berbeda, misalnya jika angka 1 ingin diletakkan di baris kedua bagian tengah, maka jika ada kotak yang sudah ada, dia akan pindah ke 2 kotak di atasnya. (bukan turun ke bawah 1 kotak).. Sulit juga ya dijelaskan di sini, sebaiknya, lihat sumbernya langsung di wikipedia. Di sini, tidak akan dijelaskan secara mendetail mengenai hal itu.
Fakta menarik seputar Siamese Method:
Siamese Method memiliki persamaan yang sangat mirip dengan
Pyramid Method.
Berikut adalah gambaran Pyramid Method dalam mengkonstruksi magic square:
Kontruksi 3x3 dengan Pyramid Method
Konstruksi persegi 5x5 dengan pyramid Method
Perhatikan bahwa konstruksi Pyramid dan Siamese sebenarnya serupa. Siamese perlu mengubah *starting point* untuk angka 1 jika hasilnya benar-benar ingin seperti Pyramid Method.
Doubly Even/ Lozenge Method
Caranya cukup mudah, yaitu hanya menuliskan angka secara berutuan, kemudian beberapa petak direfleksikan terhadap titik pusat.
Sebagai contoh persegi 4x4 dibentuk sbb:
 | Tuliskan 1 hingga 16 |
 | Buat tanda silang seperti yang terlihat pada gambar di samping, kemudian refleksikan setiap petak tersebut.
Perhatikan bagaimana 1, 4, 6, 7, 10, 11, 13, dan 16 bisa berpindah.
|
Persegi 8x8 dibentuk sbb:
|
 | Tuliskan 1 hingga 64 dan berurut.
|
| Buat tanda silang yang terbagi menjadi 4 bagian seperti yang terlihat pada gambar di samping, kemudian refleksikan setiap petak tersebut berdasarkan titik pusat persegi.
Perhatikan bagaimana 1, 4, 5, 8, ..., 64 bisa berpindah...
|
Sekarang, coba lakukan dengan persegi 12x12. Hasilnya sbb:
Salah satu kelemahan metode Lozenge ini adalah kita sulit menentukan pola refleksinya, terutama untuk persegi-persegi besar. Tidak ada aturan khusus yang menentukan polanya. Lebih jauh lagi, kita dapat menentukan polanya lebih dari 1 macam. Ada banyak sekali pola yang dapat dibentuk. Silakan bereksperimen sendiri. :D
Conway LUX Method
Metode ini hanya berlaku bagi persegi (4m+2) misalnya 6, 10, 14, dan seterusnya.
Metode ini menggunakan prinsip Siamese Method yang dimodifikasi..
Mengapa dinamakan LUX. Perhatikan sekumpulan array berikut.
Perhatikan urutannya. Ternyata urutan menulisnya mirip seperti kita menulis huruf L, U, dan X. Jika sudah paham konsep LUX ini, langsung saja kita ke langkah-langkah algoritma LUX method. :)
Langkah-langkahnya:
| 1. | Bagilah persegi menjadi sekumpulan petak 2x2. |
| 2. | Dari petak-petak itu, berikan tanda sbb:
(m+1) baris pertama adalah L.
1 baris berikutnya adalah U.
(m-1) baris terakhir adalah X.
Kemudian, tukarlah petak U di tengah dengan L di atasnya.
|
| 3. | Kerjakan dengan Siamese Method yang general. Angka 1 dimulai dari petak teratas.
|
Kalau dilihat dari bahasanya, mungkin pada bingung. Oleh karenanya, langsung saja kita ke contoh.
Persegi 10x10. (Artinya m=2, karena 4m + 2 = 10)
| 1. | Bagilah 10x10 menjadi sekumpulan petak 2x2.
m+1 baris pertama adalah L.
1 baris berikutnya adalah U
m-1 baris berikutnya adalah X.
Tukar U yang di tengah dengan petak di atasnya.
Proses ini menghasilkan sbb:
|
| 2. | Selanjutnya, gunakan metode Siamese untuk 5x5.
Perhatikan aturan LUX di tiap petak.
Hasil akhir persegi ajaib dengan metode LUX:
|
Strachey Method
Ini adalah metode terakhir yang akan kita bahas. Cukup ribet, namun sesungguhnya mudah. Metode ini hanya berlaku bagi persegi 4m + 2 (seperti halnya LUX), misalnya 6x6, 10x10. Metode ini juga menggunakan metode Siamese yang dimodifikasi.
Kita langsung saja gunakan contoh, untuk persegi 10x10. (m=2 karena 4m +2 = 10)
| 1. | Bagi persegi menjadi 4 bagian ABCD dengan urutan:
|
| 2. | Dengan metode Siamese, isilah:
1 s/d 25 di A
26 s/d 50 di B
51 s/d 75 di C .
76 s/d 100 di D
Hasil:
|
| 3. | Tukar m kolom pertama dari A dengan m kolom pertama dari D.
Tukar (m-1) kolom terakhir dari B dengan (m-1) kolom terakhir dari C.
Note: m=2 karena 4m +2 = 10
Hasilnya:
|
| 4. | Tukar petak barisan tengah paling kiri di A dengan sel yang sesuai di D.
Tukar petak yang tepat di tengah-tengah A dengan sel yang sesuai di D.
Akan menghasilkan hasil akhir sebagai berikut.
|
=======================================================================
CLOSING
Dalam mengkonstruksi magic square, kita menggunakan metode yang tergantung dari besaran perseginya:
1. Untuk persegi ganjil (3x3, 5x5, 7x7, ...), gunakan Siamese Method
2. Untuk persegi 4m (4x4, 8x8, 12x12, ...), gunakan Lozenge Method
3. Untuk persegi 4m+2 (6x6, 10x10, 14x14, ...), gunakan LUX atau Strachey Method
Sebenarnya, masih banyak metode lain yang digunakan untuk mengkontruksi magic square, misalnya Medjig Method, Bree/Ollerenshaw Method, dan sebagainya. Bahkan ada cara matematika tersendiri dalam mengkonstruksi magic square. Bisa kalian lihat di sumber-sumber di bawah. Lihat juga buku tentang Magic Square yang sungguh lengkap dan *bikin pusing* karya W.S. Andrews tahun 1917. Bisa kalian download di bawah ini:
Sekian dolo yach. Si pemilik blog mau kabur. :P.
Ada yang ingin ditanyakan, silakan tanya di comment di bawah aja. :)
.
atau sekitar 
, berapapun nilai N yang ingin kita ambil, asalkan 
. Silakan dicek sendiri dengan memasukkan nilai N ke fungsi di atas.. Lebih jauh, silakan kalian bereksperimen sendiri dengan memisalkan N, misalnya 3, 4, 5, dan seterusnya.. Lalu, bagaimana hasil tersebut didapat? Bagaimana tiba-tiba muncul nilai 
ini? Lihat lanjutannya di bawah. :)
dan 
.
.
.
, kita gunakan formula berikut:
.
, kita gunakan formula berikut:
= himpunan semua urutan dimana setidaknya ada 1 urutan (bola dan kotak) yang pasti cocok.
berarti himpunan semua urutan dimana urutan ke i , j , ... hingga p benar.
berarti himpunan semua urutan dimana urutan ke 2 dan urutan ke 6 pasti benar (bola 2 berpasangan dg kotak 2; bola 6 berpasangan dg kotak 6).
di mana k adalah jumlah urutan yang pasti benar.
, kita tahu bahwa dari 
.
, kita tahu bahwa dari 
.
. Oleh karenanya, 
, maka untuk nilai n mendekati tak hingga: 
. Artinya, peluangnya mendekati 
, nilai ini sudah didekati dengan baik, dan dapat kita anggap bahwa nilai n tidak memberikan pengaruh yang signifikan.