Variabel Kompleks (iv) {Review}

Post ini adalah materi review dari materi-materi bilangan kompleks sebelumnya. Karena ini adalah post berantai, diharapkan agar pembaca membaca post-post sebelumnya sbb:
(i) Mengenal Bilangan Kompleks
(ii) Dalil De Moivre
(iii) Persamaan Euler

Di post ini, kita akan me-review ketiga materi itu dalam contoh-contoh soal..
=========================================================================

BAGIAN I
REVIEW QUESTION

Agar kita lebih paham dalam materi ini, ayo kita mengulang sebentar...

1.	Diketahui . Tuliskan kembali dalam bentuk cartesius dan bentuk polar. Gambarkan dalam diagram Argand. Jawab: = = = Bentuk cartesius: = = + atau dapat ditulis saja tanpa i. = . Bentuk polar: = = = = = = . (tidak dapat disederhanakan lagi.) Note: adalah simbol lain dari , sedangkan adalah simbol lain dari .. Yang di atas maksudnya hanya sebagai informasi saja. Jadi, jangan kaget apabila simbol yang sering dipakai di sini adalah ataupun . Dipakai begitu karena penulisannya lebih singkat. Gambar dalam diagram Argand:
2.	Diketahui . Tuliskan kembali dalam bentuk polar. Jawab: . = Kita bisa saja mencari nilai dengan mengubah terlebih dahulu bentuk pembagian tersebut menjadi bentuk = (dengan cara kali sekawan).. Namun, hal tersebut akan memakan waktu *sedikit* lebih lama ketimbang jika kita menyelesaikannya dengan langsung. Ingat bahwa ada rumus: . Jadi, = = Ingatlah dalil de moivre: ... So, = = = . Dengan konsep yang sama seperti di atas, kita akan mencari (atau ) = __= __= __= __= (di sini, kita bisa memanipulasi sudut, karena dalam konsep polar.) Jadi, =
3.	Diketahui . Berapakah banyak akar kompleks dari persamaan tersebut? Tentukanlah hasil perkalian dari semua akar kompleks tersebut. Jawab: Banyak akarnya sesuai dengan pangkat tertinggi dari . Karena pangkat tertingginya 4, maka banyaknya akar kompleks juga 4. Note: ini hanya berlaku dalam konsep bilangan kompleks. Untuk mencari hasil kali akar-akarnya, kita tidak perlu mencari satu per satu nilai dari , , , dan 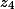. Kita cukup memakai cara cerdik. Persamaan di atas terbentuk dengan proses sbb: Dengan mengalikan seluruhnya, kita dapatkan sbb: Maka, dengan menghubungkannya ke persamaan di soal, kita tahu bahwa: Selesai.
4.	Diketahui . Tentukanlah . Jawab: Berhati-hatilah menjawab soal ini. Bilangan kompleks dapat dioperasikan dalam penjumlahan, pengurangan, perkalian, pembagian, dan pemangkatan. Namun, untuk pengakaran bilangan kompleks, hal ini masih belum dapat dipastikan, karena bentuk akarnya sulit disederhanakan atau bahkan tidak bisa disederhanakan, karena sudah menuju dimensi non-kompleks misalnya akar dari bukan lagi bilangan kompleks karena akar pangkatnya 4... Dengan demikian, jawaban dari soal di atas adalah: . SELESAI
5.	Diketahui. Tentukanlah . Jawab: Penjelasan: bentuk soal di atas merupakan perbaikan dari soal sebelumnya. Dengan demikian, di sini kita diminta menemukan semua akar kompleks dari yang banyak akarnya ada 4. Kita kerjakan soal ini seperti yang sudah kita pelajari sebelumnya, namun lebih cepat. ^^ Ruas kiri kita gunakan dalil de moivre.. Ruas kanan kita ubah menjadi polar. Lalu, kita hubung-hubungkan ruas kiri dengan ruas kanan... ____ ____ (berlaku untuk n bilangan bulat...) Jadi, kita dapatkan keempat akarya sbb: SELESAI.
6.	Diketahui . Tuliskan kembali nilai dalam bentuk cartesius dan polar. Jawab: Cukup mengingat persamaan euler, maka: (bentuk polar) (bentuk cartesius) SELESAI.. ^^

=========================================================================

BAGIAN II
APA YANG SALAH??

1.

Dari persamaan euler , kita tahu bahwa: Kita akarkan kedua ruas, maka: Namun, jika kita gunakan persamaan euler untuk menyelesaikan ruas kiri, maka hasilnya adalah -1, sehingga: -1 = 1 Mana yang salah dari proses di atas? Jawab: Bentuk soal di atas mirip bentuk ini: Jika , maka:. Ketika kedua ruas diakarkan, maka hasilnya yang kontradiksi dengan persamaan awal. Kesalahannya adalah: operasi pengakaran pada suatu variabel atau bilangan yang nilainya belum pasti, ataupun bilangan yang tanda positif negatinya belum diketahui, maka operasi pengakaran kedua ruas itu dilarang.. Artinya, kita harus selalu menghindari operasi pengakaran ini, untuk menghindari kesalahan...

2.

Dari persamaan euler , kita tahu bahwa: ... (i) ... (ii) Dengan menggabungkan pers (i) dan (ii), kita dapatkan: Kita ln-kan kedua ruas, maka: Mana yang salah dari proses di atas? Jawab: Jawabannya mudah. Bentuk di atas mirip seperti fungsi sinus maupun cosinus.. Meskipun , namun kita tidak boleh menganggap kalau , bukan?? Itu disebabkan karena fungsi merupakan fungsi PERIODIK, sama halnya seperti fungsi sinus dan cosinus. Keperiodikan dapat dilihat dari adanya elemen sinus dan cosinus di dalamnya.. Jadi, operasi menghilangkan e dari ke itu salah.. Namun, juga bisa dianggap benar kalau kita menganggap persamaan akhirnya dilihat dalam sudut pandang polar.. Jadi, dianggap benar karena dalam polar...

=========================================================================

Sekian review materi Variabel Kompleks. Ada yang ingin ditanyakan.??

Lihat juga lanjutan post ini di Variabel Kompleks (v) {Logaritma dan Pemangkatan Kompleks}..^^

Sumber: Kalkulus I (Wikaria Gazali), dosen tercinta di Universitas Bina Nusantara.. ^^, www.ariaturns.wordpress.com