Ketaksamaan Cauchy-Schwarz...(ii)

Ini adalah lanjutan dari post Cauchy-Schwarz...(i). Di post ini akan diberikan contoh-contoh soal yang *basic* mengenai Cauchy-Schwarz dan bentuk lain Cauchy-Schwarz (Engel Form).

Teorema Cauchy-Schwarz dalam bentuk Engel:

di mana

Note: maksud dari adalah . Notasi ini akan terus dipakai selama post ini.
Atau jika dijabarkan menjadi:

=========================================================================

BUKTI Ketaksamaan Cauchy-Schwarz dalam bentuk Engel

Perhatikan bentuk ketaksamaan Cauchy-Schwarz sebelumnya, yaitu sbb:

Perhatikan bahwa di sini, nilai dan tidak dibatasi (boleh positif, nol, atau negatif)

Jika kita mentransformasikan dan , maka ketaksamaan menjadi:

Perhatikan kalau di sini dan berada di bawah akar, maka dan merupakan syarat yang harus terpenuhi pada ketaksamaan di atas.

Selanjutnya, coba substitusikan dan .
Oleh karena itu sekarang ketaksamaan menjadi:

Lihat batasan dan . Keduanya mengisyaratkan bahwa nilai ( tidak boleh nol, karena pembagian dengan nol tidak terdefinisi).
Setelah disusun ulang, ketaksamaan menjadi:

di mana
TERBUKTI

Note: simbol , , , , dan seterusnya itu hanyalah simbol yang tujuannya supaya kita tahu batasan untuk tiap sukunya. Lagi-lagi, pembuktian ini sebenarnya hanya penyusunan ulang dari bentuk sebelumnya. Jadi, janganlah bingung..!!

Bentuk ini telah dikenal di Rusia jauh sebelum Engel maupun Andreescu. Tetapi istilah "Cauchy-Schwarz dalam bentuk Engel" dan "Lemma Andreescu" lebih sering dipakai di berbagai tempat. Arthur Engel mempopulerkan bentuk ini di Jerman, sedangkan Titu Andreescu membahas bentuk ini di bukunya Mathematical Olympiad Treasures. Untuk mempersingkat pengucapan, kita akan menyebutnya CS Engel.

=========================================================================

Soal-Soal *Basic* Cauchy-Schwarz

Ada banyak sekali soal yang dapat diselesaikan dengan CS Engel. Namun, kebanyakan, penyelesaiannya tidak semudah yang kita kira. CS Engel kadang digunakan setelah kita menyederhanakan bentuk soal. Kadang CS Engel juga harus dipakai dengan teorema lainnya seperti AM-GM-HM agar inequality menjadi terbukti. Di post ini hanya akan dibahas sebagian kecil dari soal-soal Cauchy-Schwarz yang ada.

1.	Jika , , dan merupakan suku-suku Real positif yang berjumlah n dengan , buktikan bahwa: Jawab: Dengan CS Engel, maka: = 8. TERBUKTI. #################################################################
2.	Misalkan dan bilangan Real positif, buktikan bahwa: Jawab: Lakukan CS Engel 2 kali: TERBUKTI. #################################################################
3.	Misalkan , , adalah bilangan Real positif dengan . Buktikan bahwa 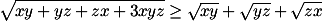Jawab: Gunakan CS biasa. 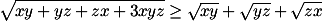Jika diuraikan, maka hasilnya: TERBUKTI #################################################################
4.	Jika , , dan bilangan Real positif, buktikan bahwa: Jawab: Dengan CS Engel, maka: Sekarang kita tinggal membuktikan Jika persamaan di atas diuraikan, maka akan ekuivalen dengan: yang bernilai benar untuk semua nilai , , dan . Maka, ketaksamaan pada soal TERBUKTI. #################################################################
5.	Jika , , dan bilangan Real positif sehingga , buktikan bahwa: Jawab: Bentuk ketaksamaan di atas dapat dibentuk dalam notasi sigma siklik (untuk menyingkat), yaitu sbb: . Soal ini dapat dikerjakan dengan berbagai alternatif. Alternatif 1: Substitusikan , , dan . Dengan demikian, ketaksamaan menjadi: (karena 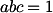) Lalu, gunakan CS Engel. . Kemudian, kita tahu dengan AM-GM, bahwa: Jadi: Maka, bentuk ini merupakan bentuk yang sesuai dengan soal. TERBUKTI. Alternatif 2 (tanpa substitusi): (dengan CS Engel) Karena , maka: . Kita kembali ke ketaksamaan sebelumnya, maka: TERBUKTI

=========================================================================

CLOSING

Akhirnya, post tentang Cauchy-Schwarz selesai juga.. Masih banyak sih soal-soal yang lain yang rumit dan ajaib.. Aku juga belum bisa terlalu banyak, terutama karena pembuktian inequality itu kerjainnya di-combo (dikerjakan bersama-sama dengan rumus yang lain). Jadi, agak sedikit rumit..

Soal-soal mengenai inequality olimpiade lainnya bisa dilihat di www.olimpiade.org. Di situ, soalnya banyak banget dan jawabannya juga variatif.. Sangat disarankan untuk belajar.. Namun, jangan langsung melihat jawabannya. Kerjakan terlebih dahulu.!! Ok.!?! ;)

Mungkin, selanjutnya di blog ini akan dibahas mengenai soal-soal inequality, dan jenis-jenis inequality lainnya.. ^^

Sumber:www.olimpiade.org, www.matriksmat.wordpress.com, http://www.mathlinks.ro/Forum/viewtopic.php?t=15125.