Bukti Limit sin x/x = 1 (x->0)

Teorema:

.

Berikut akan dibuktikan teorema ini tanpa menggunakan dalil L'Hospital.

=========================================================================

BUKTI I:

Teorema untuk setiap Perhatikan gambar di samping. !! x direpresentasikan sebagai panjang kurva (lingkaran berjari-jari 1) yang dimulai dari sumbu x positif dan berlawanan arah jarum jam. Kemudian, sin x dan tan x direpresentasikan sebagai panjang garis (lihat yang warna merah dan hijau)... Dengan demikian, teorema ini berlaku: untuk setiap
Untuk teorema di atas, kita juga dapat melihatnya dari gambar kurva f(x)=sin x, g(x)=x, dan h(x)=tan x. Lihat gambar di bawah. Di sini, kita tahu bahwa: *) untuk *) untuk

Sekarang, kita anggap bahwa x didekati dari kanan. Maka, x positif. Jadi, teorema di bawah berlaku:

Bagi dengan

Kita hitung nilai jika nilai x mendekati nol.

Oleh karena itu:

TERBUKTI

Note: Jika x didekati dari kiri, maka akan muncul seperti di bawah:

Lalu, jika x mendekati nol, maka hasil yang sama seperti di atas akan segera didapatkan.

=========================================================================

BUKTI II:

Tidak percaya dengan hasil di atas? Sekarang, kita gunakan cara primitif..!! Gunakan kalkulatormu!! Kita akan mencoba mengevaluasi nilai .
Nah, berikut adalah tabel hasil perhitungannya (4 angka di belakang koma):

x
-0.4	0.9735
-0.39	0.9748
-0.38	0.9761
-0.37	0.9773
-0.36	0.9785
-0.35	0.9797
-0.34	0.9808
-0.33	0.9819
-0.32	0.983
-0.31	0.9841
-0.3	0.9851
-0.29	0.986
-0.28	0.987
-0.27	0.9879
-0.26	0.9888
-0.25	0.9896
-0.24	0.9904
-0.23	0.9912
-0.22	0.992
-0.21	0.9927
-0.2	0.9933
-0.19	0.994
-0.18	0.9946
-0.17	0.9952
-0.16	0.9957
-0.15	0.9963
-0.14	0.9967
-0.13	0.9972
-0.12	0.9976
-0.11	0.998
-0.1	0.9983
-0.09	0.9987
-0.08	0.9989
-0.07	0.9992
-0.06	0.9994
-0.05	0.9996
-0.04	0.9997
-0.03	0.9999
-0.02	0.9999
-0.01	1
0
0.01	1
0.02	0.9999
0.03	0.9999
0.04	0.9997
0.05	0.9996
0.06	0.9994
0.07	0.9992
0.08	0.9989
0.09	0.9987
0.1	0.9983
0.11	0.998
0.12	0.9976
0.13	0.9972
0.14	0.9967
0.15	0.9963
0.16	0.9957
0.17	0.9952
0.18	0.9946
0.19	0.994
0.2	0.9933
0.21	0.9927
0.22	0.992
0.23	0.9912
0.24	0.9904
0.25	0.9896
0.26	0.9888
0.27	0.9879
0.28	0.987
0.29	0.986
0.3	0.9851
0.31	0.9841
0.32	0.983
0.33	0.9819
0.34	0.9808
0.35	0.9797
0.36	0.9785
0.37	0.9773
0.38	0.9761
0.39	0.9748
0.4	0.9735

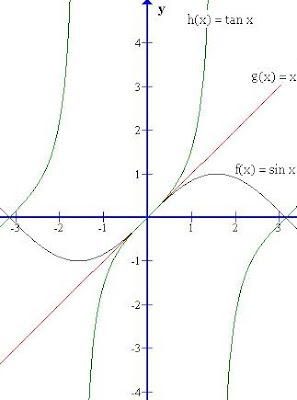
Jika masih belum puas, kita lihat saja grafik . Gambar grafiknya ditunjukkan di bawah.

Nah, ternyata untuk x mendekati nol, limitnya 1, bukan??
=========================================================================

Sumber: http://www.ies.co.jp/math/java/calc/LimSinX/LimSinX.html, dan http://planetmath.org/encyclopedia/LimitOfDisplaystyleFracsinXxAsXApproaches0.html