Ini adalah lanjutan dari post "Makanan Otak...(v) {Limit}".. Di sini, akan kuberi tahu jawaban dari 20 nomor di post itu. Namun, ada baiknya jika kalian mencoba dulu dengan usaha kalian terlebih dahulu, barulah melirik jawaban di sini untuk dicocokkan.. ^^.. Oh iya, di sini juga ada materi sekilas tentang limit, namun di sini tidak selengkap yang ada di buku text book kalian.. Namanya juga *sekilas*.. XD.
=========================================================================
Misalnya:  .
.
Namun, tidak selalu cara itu berhasil karena fungsi di titik itu tidak kontinu. Atau dengan kata lain tidak tersambung. Maka, tidak dapat terdefinisikan.
Misalnya:  . Jika nilai x langsung dimasukkan ke fungsinya, maka akan terbentuk
. Jika nilai x langsung dimasukkan ke fungsinya, maka akan terbentuk  , yang artinya tidak dapat didefinisikan. Jadi, kita harus mengubah bentuk tersebut menjadi lebih sederhana. (Lihat contoh-contoh soal di bawah).
, yang artinya tidak dapat didefinisikan. Jadi, kita harus mengubah bentuk tersebut menjadi lebih sederhana. (Lihat contoh-contoh soal di bawah).  dan
dan  juga merupakan bentuk yang tidak dapat didefinisikan.. ^^
juga merupakan bentuk yang tidak dapat didefinisikan.. ^^
Tak lupa, ada juga rumus limit untuk trigonometri untuk x mendekati nol.

Contoh limit kanan: 
Contoh limit kiri: 
Perhatikan di atas. Limit kiri dan limit kanan di titik itu sama. Jadi, fungsi itu punya limit di x=2.
Aku beri contoh..  , sedangkan
, sedangkan . Karena limit kiri dan limit kanan berbeda nilainya, maka
. Karena limit kiri dan limit kanan berbeda nilainya, maka  tidak dapat didefinisikan. Contoh lain seperti:
tidak dapat didefinisikan. Contoh lain seperti:  , sedangkan
, sedangkan . Karena nilainya berbeda, maka
. Karena nilainya berbeda, maka  tidak dapat didefinisikan.
tidak dapat didefinisikan.
Untuk mencari nilai limit, kita juga dapat menggunakan dalil L' Hospital:
 membentuk
membentuk  atau
atau  .
.
Ternyata, ada cara lain untuk mencari limit fungsi, selain yang sudah disebutkan di atas, yaitu menggunakan metode numerik (biasanya di komputer..). Dan ini juga ampuh untuk fungsi-fungsi yang susah banget disederhanakan dan dikutak-katik. Namun, kerugiannya, menimbulkan error yang relatif besar juga, tergantung seberapa akurat nilai yang kita gunakan.. Langsung ke contoh.
Tentukan nilai  .
.
Maka, kita masukkan saja nilai x yang mendekati nol. Misalkan x=0,000001. Dengan demikian:


(Untuk kasus di atas, akan lebih baik jika kita mencoret variabel x saja, maka kita akan mendapatkan nilai limitnya nol.. Namun, ada beberapa kasus di mana metode numerik sangat berperan.. :D)
=========================================================================
___***********************************************************************************1. 
Mudah dikerjakan. Hanya kita coba untuk faktorkan, kemudian, dicoret.. ^^

________________
________________
________________
***********************************************************************************2. 
Hmm.. Remember that bentuk akar sebaiknya kita kalikan dengan sekawannya.. :D

____________________
____________________
____________________
____________________
***********************************************************************************3. 
Mulanya memang agak susah, namun kita bisa menyederhanakan dengan mengeluarkan akar x-nya. Coret saja langsung akar x-nya.. :D



***********************************************************************************4. 

_______________________
_______________________
_______________________
_______________________
***********************************************************************************5._ 
Bentuk cos bisa ditransformasikan ke sin gak yach... Yupp..  .
.

_____________
_____________
_____________
_____________
Bagaimana? Apakah kalian bisa mengerjakan 20 nomor di atas dengan *sempurna*?? ^^
Btw, aku mohon maap apabila penjelasan di blog ini kurang jelas (coz, banyak cara yang di-skip juga sih..) .. Silakan kalo mo nanya, bagi yang belum mengerti.. ^^
Tuesday, December 23, 2008
Makanan Otak ...(vb) {Jawaban Limit}
Posted by
hendry_dext
--Sekilas Tentang Limit--
Sebelum melangkah lebih jauh, ada baiknya kita mengulang materi limit (yang tidak sempat kubuat materinya di blog ini...). Limit adalah suatu pendekatan. Dapat dikerjakan dengan cara memasukkan nilai pendekatan itu langsung ke fungsinya.
Subscribe to:
Post Comments (Atom)

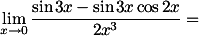

























 . Selanjutnya, bentuk ini menjadi sangat mudah dikerjakan.
. Selanjutnya, bentuk ini menjadi sangat mudah dikerjakan.






 .
.


 (wew, ternyata mudah..)
(wew, ternyata mudah..)
















 , tapi seharusnya begini:
, tapi seharusnya begini:  ..
..


 =
=














 =
=  =
=  = 0.
= 0.
 =
=






 . Maka:
. Maka:







Dik Henry, boleh minta izin untuk membuat backlink ke tulisan ini? Bukan untuk waktu dekat ini, tepatnya belum pasti, tapi minta ijin dari sekarang tidak ada salahnya...
ReplyDeleteYupp yupp yupp...
ReplyDeleteSilakan.. ^^
OMg... gw baru belajar mat.. susa amatt... ngak ngerti...
ReplyDeletetugas dari dosen, kagak ngerti neh...
ReplyDeleteizin copy pak guru, biar ilmu yg didapt bermanfaat
ReplyDelete