Sekarang kita akan mengenal dasar-dasar Summations dan Products. Jika sudah paham, tentunya kalian bisa menjawab soal-soal di bawah:
1. Apa bedanya lambang  dengan lambang
dengan lambang  ?
?
2. Apakah ?
?
3. Berapakah jumlah dari
4. Berapakah jumlah dari ?
?
5. =
=
6. A = . Hitung nilai A.
. Hitung nilai A.
7. Hitunglah
8. Hitunglah hasil dari
9. Hitunglah hasil dari
10. Hitung:
11. =
=
12.
 =
=
13. =
=
14. =
=
15. =
=
16. =
=
dan, masih banyak soal yang lainnya....
2. Apakah
 ?
?3. Berapakah jumlah dari
4. Berapakah jumlah dari
 ?
?5.
 =
=6. A =
 . Hitung nilai A.
. Hitung nilai A.7. Hitunglah

8. Hitunglah hasil dari

9. Hitunglah hasil dari

10. Hitung:

11.
 =
=12.

 =
=13.
 =
=14.
 =
=15.
16.
 =
=dan, masih banyak soal yang lainnya....
Sangat menarik, bukan?? ^^
=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=
Preface
Definisi Notasi Summations (Sigma) dan Products
Summations dan Products adalah simbol yang biasa digunakan untuk mempermudah penulisan terhadap suku-suku yang dijumlahkan atau dikalikan.Definisi Notasi Summations (Sigma) dan Products
Jika suku-sukunya ditambah, maka gunakan simbol "Summations" atau
Jika suku-sukunya dikalikan, maka gunakan simbol "Products" atau
Masih bingung? Lihat lagi penjelasan di bawah.
Sering kita jumpai penjumlahan dengan suku-suku yang sangat banyak seperti ini:

Dalam beberapa kejadian, mungkin penulisan tersebut maksudnya sudah jelas, namun sangat panjang untuk dituliskan. Untuk itulah digunakan simbol  untuk membuatnya menjadi lebih efisien, menjadi seperti berikut:
untuk membuatnya menjadi lebih efisien, menjadi seperti berikut:

Nah, penulisan dengan notasi sigma/ sum di atas lebih singkat bukan.?
Note: variabel k disebut "dummy variable" karena variabel k bisa diubah-ubah menjadi j atau simbol lainnya. Simbol ini hanya berfungsi untuk iterasi (pengulangan) saja.
Perhatikan di bawah untuk melihat contoh-contoh notasi sum/sigma dan penguraiannya.






Sudah jelas belom.?? Jadi, intinya notasi summation dipergunakan untuk mempersingkat penjumlahan suatu barisan yang panjang. ^^


Note: variabel k disebut "dummy variable" karena variabel k bisa diubah-ubah menjadi j atau simbol lainnya. Simbol ini hanya berfungsi untuk iterasi (pengulangan) saja.
Perhatikan di bawah untuk melihat contoh-contoh notasi sum/sigma dan penguraiannya.






Lalu, apa bedanya dengan products.?
Nah, kalau products (atau biasa disimbolkan dengan ) biasanya digunakan untuk suku-suku yang dikalikan. Tentunya, jika kalian tahu summations, tak akan sulit mengenal products.. Lihat contoh di bawah.
) biasanya digunakan untuk suku-suku yang dikalikan. Tentunya, jika kalian tahu summations, tak akan sulit mengenal products.. Lihat contoh di bawah.


Nah, sekarang tentunya kalian sudah tahu dong bedanya sums dengan products? ^^Nah, kalau products (atau biasa disimbolkan dengan


=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=
Bagian 2
Sifat-sifat Dasar Summations
Sifat-sifat Dasar Summations
Beberapa hal lain yang perlu diperhatikan:
Bagaimana cara mendapatkan hasil dari  ?
?
Perhatikan bahwa merupakan deret aritmatika dengan suku awalnya 1 dan beda antar sukunya juga 1. Jadi, kita dapat dengan langsung mendapatkan hasil dari notasi tersebut, yaitu:
merupakan deret aritmatika dengan suku awalnya 1 dan beda antar sukunya juga 1. Jadi, kita dapat dengan langsung mendapatkan hasil dari notasi tersebut, yaitu:

Namun, rumus ini juga dapat diperoleh dengan teknik analog (lihat bagian 3).. ^^
 ?
?Perhatikan bahwa
 merupakan deret aritmatika dengan suku awalnya 1 dan beda antar sukunya juga 1. Jadi, kita dapat dengan langsung mendapatkan hasil dari notasi tersebut, yaitu:
merupakan deret aritmatika dengan suku awalnya 1 dan beda antar sukunya juga 1. Jadi, kita dapat dengan langsung mendapatkan hasil dari notasi tersebut, yaitu:
Bagaimana cara mendapatkan hasil dari  ?
?
Seperti soal sebelumnya. Jika deret tersebut diuraikan maka menjadi:
 =
=  . Terlihat bahwa barisan tersebut adalah barisan geometri dengan suku awal a dan rasionya juga a, maka dengan mudah kita bisa menghitung hasilnya dengan rumus geometri. Jadi, hasilnya sebagai berikut.
. Terlihat bahwa barisan tersebut adalah barisan geometri dengan suku awal a dan rasionya juga a, maka dengan mudah kita bisa menghitung hasilnya dengan rumus geometri. Jadi, hasilnya sebagai berikut.
 =
= 
 ?
?Seperti soal sebelumnya. Jika deret tersebut diuraikan maka menjadi:
 =
=  . Terlihat bahwa barisan tersebut adalah barisan geometri dengan suku awal a dan rasionya juga a, maka dengan mudah kita bisa menghitung hasilnya dengan rumus geometri. Jadi, hasilnya sebagai berikut.
. Terlihat bahwa barisan tersebut adalah barisan geometri dengan suku awal a dan rasionya juga a, maka dengan mudah kita bisa menghitung hasilnya dengan rumus geometri. Jadi, hasilnya sebagai berikut. =
= 
Contoh soal:
| 1. | Hitung  . .Jawab:  = =  + +  = =  + 5. + 5.  = =  + +  = =  |
| 2. | Hitung  Jawab: Sekarang nilai variabel k dimulai dari 10. Jika kita ingin membuat nilai k menjadi 1, maka nilai batas atas dan bawah kita kurangi dengan 9, namun nilai k di dalam kurung akan berubah menjadi (k+9). Proses ini namanya shifting (menggeser). Jika kita uraikan satu per satu sukunya, maka tidak akan terjadi perubahan pada setiap sukunya.  = =  = =  = =  =  = =  |
=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=
Bagian 3
Teknik Analog
Teknik ini sangat berguna dalam mengerjakan soal seperti berikut:
 ,
,  ,
,  ,
,  , dan seterusnya.
, dan seterusnya.Semua rumus di atas dapat dicari menggunakan teknik analog. Lalu, bagaimanakah cara kerja teknik analog itu? Kita akan melihat semua penurunannya di bawah.
 dapat dicari dengan menguraikan
dapat dicari dengan menguraikan  . Berikut penurunan rumus
. Berikut penurunan rumus  .
. = 2.
= 2.  + n
+ n =
= 
Lanjut. Kita akan membuktikan rumus
 dengan menguraikan
dengan menguraikan  .
. =
= 
 =
=  +
+  +
+  +
+ 


 = 3.
= 3.  + 3.
+ 3.  + n
+ n =3.
=3. +3.
+3. +n
+n = 3.
= 3.  + 3.
+ 3.  + n
+ n = 3.
= 3. 
 = 6.
= 6. 
 = 6.
= 6. 
 =
= 
 .
.Sekarang kita akan membuktikan
 dengan menguraikan
dengan menguraikan  .
. =
= 
 =
=  +
+  +
+  +
+  +
+ 


 = 4.
= 4.  + 6.
+ 6.  + 4.
+ 4.  +
+ 
 = 4.
= 4. +6.
+6. +4.
+4. +
+
4.  + 6.
+ 6.  + 4.
+ 4.  +
+  =
= 
 + 6.
+ 6.  + 4.
+ 4.  +
+  =
= 
4.  + 6.
+ 6.  + 4.
+ 4.  + n =
+ n = 
 + 6.
+ 6.  + 4.
+ 4.  + n =
+ n = 
4.  +
+  +
+  + n =
+ n = 
 +
+  +
+  + n =
+ n = 
4.  =
= 
 =
= 
 =
= 
Contoh Soal:
| 1. | Jika A =  , ,mana yang lebih besar antara A dan B? Jawab: A =  = =  = 338350. = 338350.B =  = =  = 44100. = 44100.Jadi, lebih besar A daripada B. |
| 2. |  = =Jawab:  = =  __________________________=  __________________________=  + +  __________________________=  + +  __________________________= 333300. |
| 3. | A =  . Hitung nilai A. . Hitung nilai A.Jawab: A =   2.( 2.(  ) )_ =   2. 2. 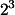 ( ( ) )_ =   2. 2. 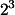  _ = 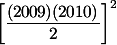  2. 2. 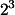  _ = 4057270425. |
=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=
Bagian 4
Sifat-Sifat Dasar Product
Seperti yang sudah dijelaskan di atas, notasi
Berikut sifat-sifat Products:
Bagian 3 di atas hanya berfungsi untuk memperjelas saja. Sifat itu juga bukan untuk dihapal, tapi untuk dipahami (toh saya pun tidak hapal) :P..| 1. |  Bukti:  = 1 = 1 |
| 2. | 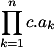 = =  dimana c adalah constanta. dimana c adalah constanta.Bukti: 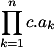 = =  = = 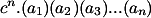 = =  |
| 3. |  = =   Bukti:  = =  = =   = =   |
| 4. |  = =  di mana c adalah konstanta. di mana c adalah konstanta.Bukti:  = =  = = 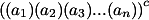 = =  |
| 5. |  = =   (ini merupakan sifat linearity) (ini merupakan sifat linearity)Bukti:  = = = =  = =   |
=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=
Bagian 5
Berpikir Kreatif Dalam menyelesaikan Masalah Deret
Mungkin ini adalah bagian yang ditunggu-tunggu oleh pembaca, yaitu mengenai pemecahan masalah secara kreatif. Kebanyakan deret diselesaikan dengan cara membuat suatu deret menjadi bentuk yang lebih umum atau mengusahakan agar suku-sukunya bisa saling meniadakan. Langsung ke masalah...! ^^Soal-Soal:
| 1. | Hitunglah  Jawab: Tidak perlu berpikir lama untuk mengerjakan soal seperti ini. Kerjakan terlebih dahulu apa yang bisa kamu kerjakan.  = =  |
| 2. |  = =Jawab: Kelihatannya sih susah. Tapi, intinya sama dengan nomor 1. Kerjakan apa yang bisa kamu kerjakan! ^^. Jadi, soal di atas, bisa disederhanakan menjadi: =  = (2+1).gif) _____  =   =  |
| 3. | Hitunglah hasil dari  Jawab: Untuk kasus deret pecahan yang membentuk deret geometri, kita bisa mengakalinya dengan mengalikannya atau membaginya dengan rasio. Pertama, anggap A =  Rasionya adalah  . Bagi A dengan . Bagi A dengan  . .Maka, 2A =  Lalu, kurangkan 2A dengan A, maka: 2A  A = A =    ____A = 1 + 1 +  ____A = 2 + 2.  ____A = 2 + 2.  ____A = 2 + 2.  ____A = 3. Hasil yang sama akan didapat jika mengalikan A dengan  . . |
| 4. | Hitunglah hasil dari  Jawab: Kita dapat menguraikan suku-sukunya.  dapat diuraikan menjadi dapat diuraikan menjadi  . Lalu, . Lalu,  dapat diuraikan menjadi dapat diuraikan menjadi  , dst. , dst.Maka, persamaan menjadi:  =  =  |
| 5. | Hitung:  Jawab: Mungkin soal ini mulanya membuat bingung. sekali lagi, kerjakan apa yang bisa kamu kerjakan. Misalnya 1+2 = 3 atau 1+2+3 = 6.. Maka, persamaan menjadi:  Keluarkan 2. =  Persamaan di atas identik dengan persamaan pada soal nomor 4. Setelah diselesaikan dengan cara nomor 4, maka ditemukan hasilnya menjadi: =  =  |
| 6. |  = =Jawab: Soal ini identik dengan soal nomor 3. Bedanya, dikerjakan secara bertingkat. Anggap: A =  Maka,  A = A =  Kurangkan A dengan  A: A:A   A = A =  Nah, bagian RHS (Right Hand Side atau ruas kanan) ternyata hasilnya sudah didapat sewaktu kita mengerjakan soal nomor 3. (Lihat nomor 3)  A = 3 A = 3A = 6. |
| 7. |   = =Jawab: Mungkin ini adalah soal yang dapat dibilang paling rumit dari semua soal yang ada di sini. Pertama, untuk mempersingkat persamaan tersebut, gunakan notasi sigma. n=2009.  = =  __________________=  __________________=  __________________=  __________________=  __________________=  __________________=  __________________=  __________________=  + +  Perhatikan bahwa hasil dari  sebenarnya sudah didapat di nomor 4 sebenarnya sudah didapat di nomor 4__________________= n +  __________________=  Karena nilai n = 2009, maka tinggal disubstitusi, maka jawabannya diperoleh.  = =  |
| 8. |  = =Jawab: Ini adalah soal yang tricky. Coba diubah dulu dalam notasi sigma. n=99.  = =  ____________=  ____________=  ____________=  ____________=  ____________=  _____________________  ) )____________=   = =  |
| 9. | Jawab: Kalikan setiap suku dengan sekawannya..  = =  x x  = =  = = 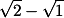  = =  x x  = =  = =   = =  x x  = =  = =  Maka persamaan pada soal menjadi: 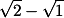 + +  + +  + ... + + ... +  Lihat suku-suku yang bisa dicoret. Jadi,  = 99. = 99. |
| 10. |  = =Jawab: Ini juga merupakan soal yang tricky. Akan sulit jika kita belum mengenal polanya. Mengingat bahwa   , maka setiap suku dalam soal bisa diubah. , maka setiap suku dalam soal bisa diubah.   Maka, persamaan yang suku-sukunya sudah diubah adalah:  Lihat suku-suku yang saling meniadakan.. Maka, jawaban dari soal di atas adalah: 2010! -1 |
=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=
Akhirnya sudah 5 hari saya begadang membuat posting ini.. Banyak dari langkah-langkah di atas yang di-reduce karena saya malas membuat gambar latex.. (setiap gambar butuh perjuangan.. >_<).. Masih banyak soal-soal deret yang lainnya (yang tentunya lebih sulit..). Semoga materi di atas dapat membantu memberi gambaran mengenai summations dan products. Yang penting kita mau belajar. ^^.. Jika ada posting yang salah, mohon diberi tahu. Saya buatnya buru-buru.
Sumber: Elementary Number Theory (Kenneth H Rosen), Olimpiade Matematika SMA (Suwah Semibiring), Olimpiade Matematika ALJABAR DAN BILANGAN (Bambang Susianto).



 =
= 
 =
= 
 =
= 



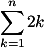 +
+ 
wah...nice post nih:)
ReplyDeletesemangat:D
pas banget!
ReplyDeletegue udah banyak lupa ma notasi sigma!
maksih yyaaaa
menarik... udah advance..
ReplyDeleteada yang bisa bantu buktikan persamaan matematika di bawah ini?
13+ 23 + 33 + … + n3 =(n (n+1))2
2
maksudnya (1 pangkat 3) + (2 pangkat 3) + (3 pangkat 3) dan seterusnya sampai (n pangkat 3) sama dengan ruas kanan dibagi 2...
terima kasih.
menarik... udah advance..
ReplyDeleteada yang bisa bantu buktikan persamaan matematika di bawah ini?
13+ 23 + 33 + … + n3 =(n (n+1))2
2
maksudnya (1 pangkat 3) + (2 pangkat 3) + (3 pangkat 3) dan seterusnya sampai (n pangkat 3) sama dengan ruas kanan dibagi 2...
terima kasih.
herueff@yahoo.com
bisa pakai metode penemuan:1 pangkat 3 = 1 = ((1x2)/2)^2
Delete1^3 +2^3 =((2x3)/2)^2
1^3+2^3+3^3 =((3x4)/2)^2
dan seterusnya.
anda juga bisa pakai induksi matematika.
menarik... udah advance..
ReplyDeleteada yang bisa bantu buktikan persamaan matematika di bawah ini?
13+ 23 + 33 + … + n3 =(n (n+1))2
2
maksudnya (1 pangkat 3) + (2 pangkat 3) + (3 pangkat 3) dan seterusnya sampai (n pangkat 3) sama dengan ruas kanan dibagi 2...
terima kasih.
herueff@yahoo.com
@Anonymous:
ReplyDeleteWew, triple post
Soal yang ditanyakan sudah dijawab di atas, yaitu di bagian teknik analog... ^^
kereeeeeeeennnnnn!!!
ReplyDeletewah...pusing gw liatnya
ReplyDeletenanya nih bung,kalo menurut kesimpulan saya,berarti untuk menyelesaikan soal2 tingkat olimpiade tentang deret tsb sangat diperlukan kreativitas?benar?
kalo gak gimana bisa kita kepikiran gimana ngubah deret nya?apa musti dikurang ato ditambah dengan angka apaan gitu..ck3
pusing deh liat nya,tapi menarik sih..cuma sedih aja gw gak bisa sekreatif itu buat menyederhanakan soal deret...huhu...
Betul.. Memang diperlukan kreativitas.
ReplyDeleteTapi, sebelum kreativitas itu muncul, diperlukan sikap ketekunan dan pantang menyerah.. ^^
muantabz tenan, aku baru engeh kamu dah posting ini. rada2 dung-deng nih liat tampilannya. tar aku pelajari dulu dech, kalo gak ngerti nanti aku tanya
ReplyDeleteda yang bisa bantu gak???
ReplyDeletemisalkan N= 1/10+2/1O^2+3?10^3+...+11?10^11
(ket: ^=pangkat ) key pliees jwb yua thax
very nice!!! nie bgt yg q cari...
ReplyDeleteinteresting.. :)
ReplyDeleteMakasih ... sangat membantu
ReplyDelete