Post ini adalah lanjutan dari posting mengenai Mengenal Bilangan Kompleks.. Sebetulnya, aku agak ragu dengan post ini. Pertama, ini adalah materi kuliah.. Pasti banyak dari kalian yang menganggap bahwa ini post yang "menyebalkan". Ada yang bilang bahwa "Matematika itu Sucks". Ada yang bilang bahwa "Matematika itu tidak penting"... Hmm.. Melalui bilangan kompleks kita bisa melihat *keistimewaan matematika* di materi ini. Persamaan euler adalah salah satu contoh hasil dari pengembangan bilangan kompleks.. Yach, bagi yang tidak mau melihat post ini, silakan ditinggalkan. Tapi, bagi yang penasaran akan *keajaiban matematika*, silakan dilanjutkan. ^^
Di sini akan dijelaskan mengenai Dalil De Moivre.. Tapi, alangkah baiknya kalau kita mengenal dulu konsep bilangan kompleks dalam polar.. ^^
=========================================================================
z = x+y dapat digambarkan dalam bidang kompleks. Artinya, kita dapat menggambarkannya secara kartesius maupun polar!! Lihat gambar di bawah untuk lebih jelasnya!
dapat digambarkan dalam bidang kompleks. Artinya, kita dapat menggambarkannya secara kartesius maupun polar!! Lihat gambar di bawah untuk lebih jelasnya!
Jika titik z digambarkan secara kartesius tentunya kita akan mengatakan bahwa titik itu berada di koordinat (x,y). Namun, jika berbicara di koordinat polar, kita akan mengatakan bahwa titik z berada di (r,



mod.(z)= r
arg.(z) =
Kembali lihat gambar di atas.


z_= x+y
z_= 
z_= 
Disingkat menjadi
z = 
Dapat dikatakan juga:
 secara geometris dapat dinyatakan cengan vektor posisi.!!
secara geometris dapat dinyatakan cengan vektor posisi.!!
Operasi bilangan kompleks secara geometris dalam bentuk vektor dapat dilakukan sebagai berikut (z1 dan z2 diketahui):
=========================================================================
Misalkan kita punya bilangan kompleks z1 dan z2 dimana:

Sekarang, kita akan mencoba mengalikan keduanya...


Lihatlah bagian yang bisa digabung.... Lalu, persamaan itu *secara ajaib* menjadi:

Disingkat menjadi:

Dengan sendirinya, 
 .
.
Jika  , maka kita akan menemukan dalil de Moivre:
, maka kita akan menemukan dalil de Moivre:
n bilangan bulat.. .. Cobalah sendiri.. ^^
.. Cobalah sendiri.. ^^
Catatan: Perkalian-perpangkatan/pengambilan akar-pembagian bilangan-bilangan kompleks akan cepat dilakukan dengan menggunakan sistem polar, apabila argumen-argumen bilangan kompleks tersebut merupakan sudut-sudut kelipatan dari  atau
atau  .
. .
.
Hitunglah  .
.
Jawab:
Seandainya kita tidak mau menggunakan dalil de Moivre pun, kita bisa mengerjakan soal ini secara *tradisional*.. Yaitu dengan mengalikannya satu per satu. =
=  =
=  =
= 
Nah, bagaimana jika kita ingin mengerjakannnya secara dalil de Moivre? Akan lebih mengerti jika kita menggambar titik z itu.. (Ini supaya kita lebih mengerti saja.. Tapi, tidak mutlak) =
= 
 ---->
---->  (karena terletak di kuadran 4...)
(karena terletak di kuadran 4...)

 =
=  .
.
Hasilnya sama, bukan?
Contoh Soal 2:
Hitunglah  .
.
Jawab:
Soal di atas dapat dikerjakan dengan mengalikan z sebanyak 7 kali.. Tapi, itu sangat buang-buang waktu.. Jadi, kita akan menggunakan dalil de Moivre..
Langkahnya sama seperti nomor 1. Hitung r dan 



Jadi,


 .
.
Contoh Soal 3:
Tentukan nilai z.
Jawab:
Masih ingatkan notasi ini:  .
.
Hal ini juga berlaku untuk  , maka persamaan di atas menjadi
, maka persamaan di atas menjadi
Soal di atas dapat ditulis dalam bentuk:  .
.
 +
+  (di mana n =0,1,2,3,...)
(di mana n =0,1,2,3,...)
Ingat Dalil De Moivre  .. Jika n=3, maka:
.. Jika n=3, maka: --->
--->  --->
--->  --->
--->  .
. --->
--->  --->
--->  =
=  --->
---> 
Oleh karena itu, kita sekarang sudah mendapatkan z.
z =  =
=  =
=  .
.
Dengan mensubstitusikan nilai n=0,1,2, maka kita akan mendapatkan 3 nilai z. =
=  =
=  = 2
= 2 =
=  =
=  =
= 
 =
=  =
=  =
= 
=========================================================================
Selesai sudah bagian Dalil De Moivre, bilangan kompleks bagian kedua...!! XD
Mudah bukan?? Post ini adalah revisi kedua, setelah sebelumnya ada kesesatan menggunakan dalil De Moivre di mana nilai n-nya boleh pecahan (di contoh soal nomor 3 dan 4).. Ingat, dalil de Moivre hanya berfungsi jika n adalah bilangan bulat.. So, post ini aku rombak ulang agar tidak menggunakan cara yang menyesatkan (meskipun jawaban di post sebelumnya tidak salah, namun ini hanya di dalam kasus khusus yang demikian, dan tidak akan dibahas di sini.) ^^
Lihat juga post berikutnya tentang "Bukti: Persamaan Euler"
Ada yang ingin ditanyakan??
Sunday, December 14, 2008
Bilangan Kompleks... (ii) {Dalil De Moivre}
Posted by
hendry_dext
BAGIAN III
BILANGAN KOMPLEKS DALAM POLAR
Perhatikan post sebelumnya!!Notasi:
Oleh karena itu,
Lihat kembali gambar di atas, bilangan kompleks z = x+y
BAGIAN IV
DALIL DE MOIVRE
Dengan sistem polar mempermudah perkalian dan pembagian bilangan-bilangan kompleks.Note: Bagaimana jika kita melakukan pembagian bilangan kompleks z1 dan z2? Maka, akan menghasilkan rumus:
Contoh Soal 1:r =
Sumber: Kalkulus I (Wikaria Gazali), dosen tercinta di Universitas Bina Nusantara.. ^^
Subscribe to:
Post Comments (Atom)





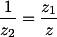







shit man
ReplyDeleteAw. itu juga pengarang terfavorit ku (u/ pengarang texbook di Indonesia :P) saya suka bukunya yang berjudul "Kalkulus Lanjut".. hahah.. teruskan bro
ReplyDeletewooooooooooooo
ReplyDeletekkereeeen !!
nice info. tolong buktiin donk
ReplyDelete|z1| - |z2| <= |z1+z2|
dan
|z1+z2| <= |z1|+|z2|
Bingung
ReplyDeleteMohon maaf. Itu Contoh soal nomor 2 kayanya ada yang salah..
ReplyDeleteBukan kah sin 60 itu 1/2. Dan jawaban terakhir bukan kah 64 akar 3. Hehe..
Thank banget, sangat membantu.
ReplyDeleteThanks for sharing thhis
ReplyDelete