Soal-soal berikut memiliki bentuk yang berbeda-beda, namun sebetulnya serupa. Mari kita lihat.
| 1. | Tentukan perbandingan jari-jari lingkaran A, jari-jari lingkaran B, dan jari-jari lingkaran terpotong dengan pusat O. |
| 2. | R adalah jari-jari setengah lingkaran dengan pusat A, sedangkan r adalah jari-jari lingkaran dengan pusat B. Jika BC tegak lurus AC, r=5, dan R=7, hitunglah a. |
| 3. | Perbandingan jari-jari seperempat lingkaran B dengan jari-jari lingkaran A adalah 2:3. Jari-jari setengah O adalah 10 cm. Berapakah luas yang diarsir? |
| 4. | Jari-jari setengah lingkaran O adalah 15 cm. Jari-jari setengah lingkaran A adalah 10 cm. Jari-jari setengah lingkaran B adalah 5 cm. Tentukan jari-jari lingkaran C. |
| 1. | Kita buat kembali gambarnya sbb. Karena  , maka , maka   , maka , maka         kuadratkan.    kuadratkan lagi.    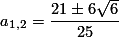 Pilih  karena karena  Jadi, perbandingan ketiga jari-jari  ______________________________________  |
| 2. | Kita gambarkan kembali soal nomor 2. Seperti diketahui di soal:  dan dan  . .Yang krusial di sini adalah kita harus membuat titik pusat lingkaran O. Maka, kasus ini akan menjadi sangat mudah.             |
| 3. | Soal ini mirip dengan dua soal sebelumnya. Pertama-tama, kita gambar ulang. Langsung saja kita ke inti penyelesaian.  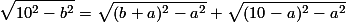   , maka kita misalkan , maka kita misalkan  dan dan  .. ..     . .     karena karena  harus positif. harus positif.Maka, luas yang diarsir  _____________________  _____________________  _____________________  cm2 cm2 |
| 4. | Tidak jauh berbeda dengan soal-soal sebelumnya.. Perhatikan               |
=======================================================================
Dapat kita lihat bahwa soal-soal tersebut sekilas memang berbeda, namun dikerjakan dengan cara yang serupa.. Soal mengenai lingkaran di atas juga sering keluar dalam seleksi awal olimpiade, dan sering menghabiskan waktu bagi peserta yang belum pernah mengerjakan sebelumnya.
Jadi, jika kalian sudah mengetahui model-model soal semacam ini dan menemukannya di soal pada awal seleksi olimpiade, anggap saja sebagai soal bonus. :)
Jadi, jika kalian sudah mengetahui model-model soal semacam ini dan menemukannya di soal pada awal seleksi olimpiade, anggap saja sebagai soal bonus. :)
Sumber:
1. Buku "Kumpulan Soal Unik Matematika" oleh Tobi Moektijono.
2. Buku "Olimpiade Matematika untuk SMU" oleh Suwah Sembiring.
1. Buku "Kumpulan Soal Unik Matematika" oleh Tobi Moektijono.
2. Buku "Olimpiade Matematika untuk SMU" oleh Suwah Sembiring.










tanya ya...
ReplyDeleteitu yang nomor 2 dapat petunjuk dari mana yang harus dicari itu DO, OC, AC, OB ? Makasih...
Itu harus dicari karena:
ReplyDelete1. Biasanya untuk mengerjakan soal lingkaran, carilah jari-jari dahulu, dan jarak antar titik pusat lingkaran dengan titik pusat lingkaran.
2. Balik lagi ke pertama.
3. Kalau bingung menentukan mana yang harus dicari, carilah semua yang bisa dicari.
:)