Berikut adalah rumus-rumus dasar turunan/ derivatif:
Bila y=f(x) , y'=f'(x), dan a adalah konstanta maka:
| _ |
|
=========================================================================
Mengapa Turunan dari  adalah
adalah  ?? (a konstanta)
?? (a konstanta)
Bukti ini sangat mudah. Langsung kita gunakan definisi dari derivatif. adalah
adalah  ?? (a konstanta)
?? (a konstanta) (atau bisa kita gunakan cara seperti di post "bukti sifat-sifat turunan" yang dilakukan secara bertahap..)
(atau bisa kita gunakan cara seperti di post "bukti sifat-sifat turunan" yang dilakukan secara bertahap..) .
.









TERBUKTI
Selanjutnya: Mengapa turunan dari  adalah
adalah  ??
??
Kita bisa saja menguraikan penurunan rumus ini dari awal, seperti cara yang serupa seperti di atas. Namun, kita gunakan saja rumus sebelumnya, untuk membuktikan rumus ini., supaya kita tidak 2 kali kerja.. adalah
adalah  ??
??
Di atas merupakah rumus yang sudah kita dapatkan sebelumnya. Substitusikan a=e.

 =
=  , maka:
, maka:
TERBUKTI
Mengapa turunan dari  adalah
adalah  ??
??
 adalah
adalah  ??
??







TERBUKTI
Mengapa turunan dari  adalah
adalah  ?? (a konstanta)
?? (a konstanta)
 adalah
adalah  ?? (a konstanta)
?? (a konstanta)





TERBUKTI
Selanjutnya: Mengapa turunan dari  adalah
adalah  ??
??
Sesuai dengan rumus sebelumnya: adalah
adalah  ??
??


TERBUKTI
Mengapa turunan dari  adalah
adalah  ??
??
Untuk membuktikan ini, kita bisa gunakan definisi awal dari derivatif. adalah
adalah  ??
?? .
.


==> Note: rumus di atas HARUS dapat diturunkan sendiri.
Dengan demikian, persamaan
 menjadi:
menjadi:





TERBUKTI
Mengapa turunan dari  adalah
adalah  ??
??
Pembuktiannya menggunakan cara yang sama seperti di atas. adalah
adalah  ??
??



==> rumus di atas HARUS bisa diturunkan sendiri.
Dengan demikian, persamaan
 menjadi:
menjadi:





TERBUKTI
Note: Cara lain menurunkan turunan sin x dan cos x yaitu dengan melihat identitas eulernya (Lihat di sini):
*)

*)

Dengan menurunkan sisi ruas kanan dari
 , maka akan menghasilkan sisi kanan dari
, maka akan menghasilkan sisi kanan dari  .
.Mengapa turunan dari  adalah
adalah  ??
??
Fungsi tangen dapat dibentuk ke dalam bentuk pembagian. adalah
adalah  ??
??
Kemudian, ingatlah sifat turunan berikut.

Dengan menggunakan sifat itu, maka pembuktian turunan f(x) akan segera terbukti.




TERBUKTI
Rumus-rumus di atas adalah rumus turunan yang siap pakai. Selanjutnya, akan dibahas pembuktian untuk rumus-rumus yang kurang begitu *terpakai*. Jika terpakai pun, kita dapat dengan mudah menurunkannya. Konsep menurunkannya sama seperti di atas, kecuali adanya beberapa yang mengharuskan substitusi trigonometri.. But, lagi-lagi, rumus di bawah jangan sengaja dihapal (kecuali kalau tidak sengaja terhapal).. ;P
Bukti: turunan dari  ,
,  , dan
, dan 
Bukti bisa menggunakan teorema sebelumnya yang berbunyi:  ,
,  , dan
, dan 
 .
.Sama halnya seperti menggunakan dalil rantai...



Dengan aturan rantai, maka:







TERBUKTI
Bukti turunan dari fungsi arcsin x, arccos x, arctan x, etc
Tidak semua bukti akan diberikan di sini, karena prosesnya hampir sama. Dan, akan terlalu banyak jika semuanya dibahas dalam satu post di blog. So, it is your challenge to prove it by yourself...Bukti turunan dari fungsi arcsin x




Dengan menggambar segitiga siku-siku dengan sudut y (memisalkan sisi depan adalah x, sisi miring 1), maka kita akan mendapatkan cos y. (Lihat gambar)
Atau, kita bisa memanfaatkan identitas trigonometri: , maka:
, maka:
 .
.
Di sini, kita dapat: Atau, kita bisa memanfaatkan identitas trigonometri:
 , maka:
, maka: .
. . Maka, tinggal disubstitusikan...
. Maka, tinggal disubstitusikan...
TERBUKTI




 , maka
, maka  .
.Gambarkan segitiga siku-siku dengan sudut y. Misalkan sisi depan adalah 1, dan sisi samping adalah x. (lihat gambar).
Dengan demikian, kita bisa menghitung panjang sisi miring, kemudian menghitung nilai dari sin y.



TERBUKTI
Bukti turunan dari fungsi hiperbolik: sinh x, cosh x, etc
Pembuktiannya menggunakan sisi kanan dari identitas terhadap euler. Ingat bahwa:


Bukti turunan sinh x
 (TERBUKTI)
(TERBUKTI)Bukti turunan cosh x
 (TERBUKTI)
(TERBUKTI)Bukti turunan tanh x

___________
 (TERBUKTI)
(TERBUKTI)=========================================================================
Masih banyak bukti yang belum dibuktikan karena keterbatasan waktu.. Namun, prosesnya tidak berbeda jauh seperti pembuktian di atas.. Jika ada yang merasa kesulitan, silakan bertanya di comment.. ^^
Btw, thx for www.ariaturns.wordpress.com because having inspired me writing this topic. ^^
Sumber: www.ariaturns.wordpress.com, Kalkulus I (Wikaria Gazali): Graha Ilmu.









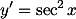




































wich..rajin eng si abang...ane salut
ReplyDeletenuhun ach..keep posting :)
yang aku tanya bukan masalah nurunin rumus, tapi naikin semangat ngulik matematikanya :)
kalo bertebaran posting yng kyk beginian, mgkn negara qt bakal punya jagoan2 d bdng matmtka....thx a lot ych,,aplikasi byk bgt bwt khdpn keseharian.like me as civil engineer...keep posting..... :)
ReplyDeletehem...sudah lupa semua, soalnya sudah 18 tahun mengajar SMP, and baru aja belajar ngeblok..salam kenal
ReplyDeletemas. tolong dong bantuin. e itu apa sih?? knp bs = 2,718.....
ReplyDeletee itu konstanta euler.
ReplyDeleteUntuk mendapatkan 2,718... itu menggunakan perhitungan mesin (kalkulator)..
Coba saja kamu hitung berapakah hasil dari:
(i) (1,001)^1000
(ii) (1,0001)^10000
(iii) (1,00000000001)^100000000000
dst...
Maka, hasilnya akan mendekati 2,718...
Waduh..
ReplyDeletemembuktikan arc tan nya bingung nih,...
T_T
thx, sangat membantu....keep on posting :)
ReplyDeleterumus euler tuh dri mana?.. kok tiba2 bisa jadi rumus gitu???
ReplyDeleteRumus euler yang mana ya? Euler ada banyak rumusnya.. >___<. Jadi, binun..
ReplyDeletewoow,, makasih mas hendry,,,
ReplyDeletehahaha pelajaran smu nih dah rada2 lupa...
untung ada nihhh... buat tugas kul...
thankkkssss
nanya doonk klo turunnya e^-x apa?
ReplyDeletehahaha
Bang Hendry, tlng bktiin dong klu (f(x+h)-f(x))/h = ax^(n-1)
ReplyDeleteIlmu sya msh rndah nih..
klo turunannya arc cos 1/x gmn??
ReplyDeletebagaimana membuktikan tanh(x1+x2)= tanh(x1)+tanh(x2)/1+tanh(x1)tanh(x2)?
ReplyDeletewaaah....marvelous nih posting...!!! Hebat!!! :D :D :D
ReplyDeletemateri pemodelan diferensial parsial dawai berfibrasi kalo bsa ditampilkan
ReplyDeleteTerima kasih banyaaaakkk :)
ReplyDeletemakasih pak, ngebantu kalkulus ni rangkuman
ReplyDeletepak mjnta izin ngopy paste dokumen ini,
ReplyDeleteterimakasih sebelumnya,sangat ngebantu kalkulus ana
ReplyDeletemaksih banyak,membantu sekali
ReplyDeletethanks ya
ReplyDeleted/dx 4x(pangkat 3) + 2x (pangkat 2) + 2x
ReplyDeletejwbnnya gmna nih ?
sangat membantu, terimakasih banyak,, :)
ReplyDeleteHarus di bookmark nih postingan klo perluane save page as
ReplyDeletegan minta tolong postingkan tabel rumus diferensiasinya klw ad?
ReplyDeleteGan gimana ya caranya supaya gampang faham ama rumus matematika, soalnya ane susah banget ngertinya klo belajar matematika. ..
ReplyDeletePencerahan nya Gan,,,
klo sinh(a-b)=...
ReplyDeleteterimakasi ..
tolong buktiin ya rumus a^n=n.a^n-1
ReplyDeleteThat's cool (y) (y)
ReplyDeleteMakasih banyak kak, lengkap ._.
ReplyDeleteCrownQQ Agen DominoQQ BandarQ dan Domino99 Online Terbesar
ReplyDeleteYuk Buruan ikutan bermain di website CrownQQ
Sekarang CROWNQQ Memiliki Game terbaru Dan Ternama loh...
10 permainan :
=> Poker
=> Bandar Poker
=> Domino99
=> BandarQ
=> AduQ
=> Sakong
=> Capsa Susun
=> Bandar 66
=> Perang Baccarat
=> Perang dadu (NEW GAME)
Promo Yang berlaku
=> Bonus Refferal 20%
=> Bonus Turn Over 0,5%
=> Minimal Depo 20.000
=> Minimal WD 20.000
=> 100% Member Asli
=> Pelayanan DP & WD 24 jam
=> Livechat Kami 24 Jam Online
=> Bisa Dimainkan Di Hp Android
=> Di Layani Dengan 5 Bank Terbaik
=> 1 User ID 10 Permainan Menarik
=> Menyediakan deposit Via Pulsa
Link Resmi CrownQQ:
- mastercqq.com
- mastercqq.net
- mastercqq.org
Info Lebih lanjut Kunjungi :
Website : CrownQQ
WHATSAPP : +6287771354805
Line : CS_CROWNQQ
Facebook : CrownQQ Official
Kemenangan CrownQQ : Agen BandarQ