Sajak Untuk Menghapal Pi.. ^^

Sir, I bear a rhyme excelling
In mystic force and magic spelling
Celestial sprites elucidate
All my own striving can't relate

Tahukah kamu untuk apakah sajak di atas digunakan? (Lihat kembali judul di atas.. ^^). Sajak di atas merepresentasikan digit-digit pi () yang bernilai 3,14159 26535 89793 23846. Eitss.. Kalian bisa menemukan sajak-sajak lain (atau mungkin cerita) yang akan membuatmu terkagum-kagum.. Lihat lanjutan post di bawah.. ^^

=========================================================================

PI MNEMONICS

3,14159 2

How I wish I could calculate pi.

3,14159 26

May I have a large container of coffee?

3,14159 26

Can I have a small container of coffee?

3,14159 26535 89

See, I have a rhyme assisting
my feeble brain, its tasks
oft-times resisting.

3,14159 26535 897

How I wish I could recollect of circle round
The exact relation Archimede unwound.

3,14159 26535 89793 23846

Sir, I wish I could determine pi
Eureka! cried the great inventor
Christmas pudding, Christmas pie
Is the problem's very center.

3,14159 26535 89793 23846 26433 83279

Sir, I send a rhyme excelling
In sacred truth and rigid spelling
Numerical sprites elucidate
for me the lexicon's full weight.
If nature gain, who can complain
tho' Dr Johnson fulminate.

Sir, I bear a rhyme excelling
In mystic force and magic spelling
Celestial sprites elucidate
All my own striving can't relate.
Or locate they who can cogitate
And so finally terminate.

But a time I spent wandering in bloomy night;
Yon tower, tinkling chimewise, loftily opportune.
Out, up, and together came sudden to Sunday rite,
The one solemnly off to correct plenilune.

Now I will a rhyme construct
By chosen words the young instruct.
Cunningly devised endeavour,
Con it and remember ever.
Widths of circle here you see.
Sketched out in strange obscurity.

Now I, even I, would celebrate
In rhymes inapt, the great
Immortal Syracusan, rivaled nevermore,
Who in his wondrous lore,
Passed on before,
Left men his guidance
How to circles mensurate.

See, I have a rhyme assisting
My feeble brain, its tasks sometime resisting,
Efforts laborious can by its witchery
Grow easier, so hidden here are
The decimals all of circle's periphery.

3,14159 26535 89793 23846 26433 83279 5

Sir: I wish I could recapture my memory about Sir
Jeans' diabolic mnemonics! However, invention
now of any reliable easy phrase is beyond what shy
and fumbling aid my present intellect gives.

May I have a month, professor,
To figure these, you brain assessor?
Calculate, student, calculate now!
As the figuring gets longer,
My friend, hope you get stronger
And no figures incorrect allow!

You I sing, O ratio undefined
By strict assay and lined,
Sequence limitless. Stunned regarding you,
We see eternity -- alas -- unwind
In random cast and rue,
Dejected out of measure, reckoning blind.

May I tell a story purposing to render clear
the ratio circular perimeter-breaths, revealing
one of the problems most famous in modern days,
and the greatest man of science anciently known.

3,14159 26535 89793 23846 26433 83279 50288 41971 69399 37510 58209 74944 59230 78164 06286 20899 86280 34825 34211 70679 82148 08651 32823 06647 09384 46095 50582 23172 53594 08128 48111 74502 84102 7

How I need a drink, alcoholic of course, after the tough lectures involving quantum mechanics; but we did estimate some digits by making very bad, not accurate, but so goddamn efficient tools! By dropping valuable wood, a dedicated student, I, Volokh, Alexander, can determine beautiful and curious stuff, O! Smart, gorgeous me! Descartes himself knew wonderful ways that could ascertain it too! Revered, glorious - a wicked dude! Behold an unending number: pi! Thinkers' ceaseless agonizing produces little, if anything! For this constant, it stops not -- just as e, I suppose. Vainly, ancient geometers computed it -- a task undoable. Legendre, Adrien Marie: "I say pi rational is not!" Adrien proved this theorem. Therefore, all doubters have made errors. (Everybody that's Greek.) Today, counting is as bad a problem as years ago, maybe centuries even. Moreover, I do consider that variable x, y, z, wouldn't much avail. Pi, imaginary, like i? No, buffoon!

3,14159 26535 89793 23846 26433 83279 50288 41971 69399 37510 58209 74944 59230 78164 06286 20899 86280 34825 34211 70679 82148 08651 32823 06647 09384 46095 50582 23172 53594 08128 48111 74502 84102 70193 85211 05559 64462 29489 54930 38196 44288 10975 66593 34461 28475 64823 37867 83165 27120 19091 45648 56692 34603 48610 45432 66482 13393 60726 02491 41273 72458 70066 06315 58817 48815 20920 96282 92540 91715 36436 78925 90360 01133 05305 48820 46652 13841 46951 94151 16094 330

For a time I stood pondering on circle sizes. The large computer mainframe quietly processed all of its assembly code. Inside my entire hope lay for figuring out an elusive expansion. Value: pi. Decimals expected soon. I nervously entered a format procedure. The mainframe processed the request. Error. I, again entering it, carefully retyped. This iteration gave zero error printouts in all - success. Intently I waited. Soon, roused by thoughts within me, appeared narrative mnemonics relating digits to verbiage ! The idea appeared to exist but only in abbreviated fashion - little phrases typically. Pressing on I then resolved, deciding firmly about a sum of decimals to use - likely around four hundred, presuming the computer code soon halted! Pondering these ideas, words appealed to me. But a problem of zeros did exist. Pondering more, solution subsequently appeared. Zero suggests a punctuation element. Very novel! My thoughts were culminated. No periods, I concluded. All residual marks of punctuation = zeros. First digit expansion answer then came before me. On examining some problemsunhappily arose. That imbecilic bug! The printout I possessed showed four nine as foremost decimals. Manifestly troubling. Totally every number looked wrong. Repairing the bug took much effort. A pi mnemonic with letters truly seemed good. Counting of all the letters probably should suffice. Reaching for a record would be helpful. Consequently, I continued, expecting a good final answer from computer. First number slowly displayed on the flat screen - 3. Good. Trailing digits apparently were right also. Now my memory scheme must probably be implementable. The technique was chosen, elegant in scheme: by self reference a tale mnemonically helpful was ensured. An able title suddenly existed - ``Circle Digits". Taking pen I began. Words emanated uneasily. I desired more synonyms. Speedily I found my (alongside me) Thesaurus. Rogets is probably an essential in doing this, instantly I decided. I wrote and erased more. The Rogets clearly assisted immensely. My story proceeded (how lovely!) faultlessly. The end, above all, would soon joyfully overtake. So, this memory helper story is incontestably complete. Soon I will locate publisher. There a narrative will I trust immediately appear, producing fame. THE END..

=========================================================================

CLOSING

Sajak yang terakhir adalah sajak yang memuat 403 digit di belakang pi. Sajak itu ditulis di sebuah buku yang berjudul "The Mathematical Intelligencer", volume 8 no.3, halaman 56-57.. (but, aku gak yakin siapa penulisnya..). Bilangan nol (0) direpresentasikan dengan tanda baca lain selain single dot (.) seperti tanda seru (!), maupun 2 titik(..). Jika ada beberapa kata yang lebih dari 9 huruf, itu merepresentasikan 2 digit. Misalnya, "abbreviated" merupakan representasi terhadap digit "11".

Masih banyak sajak "Pi Mnemonics" yang lain yang tersebar di web. Silakan lihat bagian sumber di bawah untuk melihat referensi yang lebih lengkap. Sajak itu juga tidak hanya dalam bahasa Inggris, tapi juga ada dalam bahasa Spanyol, Romanian, Portugis, dan sebagainya. Namun, alangkah sayangnya. Belum ada sajak Pi dalam bahasa Indonesia (tentunya kita akan kesulitan dalam menemukan kata yang terdiri hanya 1 huruf..)

Sebenarnya, sajak di atas bukanlah untuk dihapal, terutama untuk sajak dengan 402 digit. Siapa yang mau menghapalnya??? Yah, kecuali jika kalian merupakan maniacs "Pi".. :P

Sumber: http://vagrantcafe.com/forum/showthread.php?t=19715&page=2, http://pages.intnet.mu/cueboy/education/maths/pi/england.htm, http://www.uz.ac.zw/science/maths/zimaths/pimnem.htm, and http://www.komplexify.com/math/humor_pure/PiMnemonics.html.

Click Here to Read More..

Secret of The "1 3 5 7" Game Revealed

Ini adalah lanjutan dari post "Secret of The 1357 Game".. Silakan dibaca lagi, bagi yang belum tahu bagaimana memainkan permainan ini..

Sebelumnya, maap kalau aku post-nya lama.. Mungkin beberapa dari kalian sudah penasaran.. Hahaha. Di sini, akan kuberi tahu trik untuk selalu bisa memenangkan permainan ini. (Namun, ada beberapa perkecualian yang tidak selalu).. Ayo, lanjutkan membaca.. ^^

=========================================================================

== HERE'S THE SECRET ==

Perhatikan kombinasi kumpulan kelereng ini.. Kombinasi inilah yang akan membuatmu menang.
Intinya, usahakan membuat kombinasi ini di setiap giliranmu.!! Jika musuhmu menemui kombinasi kelereng ini pada giliran dia sebelum dia mengambil kelereng, maka dia tidak akan berkutik.

No.	Kombinasi yang menyebabkan musuh kalah (Pola/Posisi Kalah)	Ilustrasi kombinasi
1.	Kumpulan ganjil dari 1 1, atau 1-1-1 atau 1-1-1-1-1 atau 1-1-1-1-1-1-1, dan seterusnya...	atau dan seterusnya
2.	angka kembar (tidak boleh 1-1) 2-2 atau 3-3 atau 4-4, dan seterusnya	, atau , dan seterusnya...
3.	Angka triple dimulai dengan 1 1-2-3 atau 1-4-5 atau 1-6-7, dan seterusnya...	, atau , dan seterusnya....
4.	Triple yang lain: 2-4-6, atau 2-5-7, atau 3-4-7, atau 3-5-6	atau dan seterusnya...
5.	Kombinasi dari angka kembar dengan angka kembar (tidak boleh 1-1-1-1) Misalnya: 1-1-2-2 atau 1-1-3-3, atau 1-1-4-4, atau 1-1-5-5, atau 2-2-3-3, atau 2-2-5-5, atau 4-4-4-4, dan seterusnya...	atau dan seterusnya...
6.	1-3-5-7
7.	Masih banyak lagi kombinasi yang mungkin, namun aturan lain tidak dibahas lebih lanjut karena tidak dibutuhkan dalam game yang relatif simple ini.

Tabel ini tidak dibuat berdasarkan rumus, tapi *pengalaman bermain*. Semakin sering kamu bermain, maka pola ini dengan sendirinya akan dapat diketahui.

Lihat, yang nomor (6) di atas, ternyata pola 1-3-5-7 adalah pola kalah. Jadi, game ini dapat selalu dimenangkan apabila kita jalan pada giliran kedua. Namun, apabila kita mengambil pertama kali, maka peluang menang sesungguhnya tetap ada jika musuh tidak mengetahui strategi ini.. Kesempatan menang akan selalu ada jika kita selalu mengusahakan kombinasi-kombinasi di atas (sebelum musuh menyadarinya).. ;-)

Agar lebih jelas, mari kita lihat bagaimama simulasi game ini..

=========================================================================

== SIMULASI 1-3-5-7 ==

Nah, di sini, anggap saja kita sebagai Budi, sedangkan musuhnya adalah Anto.. Anggap Anto jalan terlebih dahulu.. Di sini, kita (Budi) akan menerapkan strategi 1-3-5-7 sepenuhnya..

Anto jalan pertama kali. Anto mengambil 2 kelereng dari kelompok 2.
Nah, sekarang giliran kita (Budi) yang jalan.. Kita harus mengambil 2 kelereng di kelompok 4, karena akan menyisakan 1-1-5-5.. 1-1-5-5 adalah posisi kalah (lihat kembali kombinasi di atas) Note: kadang di game ini kita perlu mengecoh. Misalnya Budi berkata, "Wah, kamu mengambil 2.. Kalau begitu saya juga ambil 2 ahh."..
Anto, yang tidak dapat berkutik, mengambil 1 kelereng di kelompok 1.
Giliran Budi: Yang tersisa sekarang adalah 1-5-5. Budi punya 2 alternatif yang akan membuatnya menang. Pertama, ambil 1 kelereng di kelompok 1, ini akan menyisakan 5-5. Kedua, ambil 1 kelereng di kelompok 2, ini akan menyisakan 1-4-5. 5-5, dan 1-4-5 adalah posisi kalah (lihat di atas) Di sini, Budi mengambil alternatif yang kedua sehingga menyisakan 1-4-5.
Lagi-lagi, sekarang Anto berada di posisi kalah dan tidak dapat berkutik. Dia mengambil 3 kelereng di kelompok 3.
Giliran Budi: Kelereng yang tersisa adalah 1-4-2. Ambil 1 kelereng di kelompok 2 sehingga akan menyisakan 1-3-2 (kombinasi dari 1-2-3) 1-2-3 adalah posisi kalah (lihat aturan di atas)
Anto mengambil 1 kelereng di kelompok 2.
Giliran Budi: Kamu seharusnya sudah tahu apa yang harus kamu lakukan. Ambil 1 kelereng di kelompok 1, sehingga akan menyisakan 2-2. 2-2 adalah posisi kalah.
Anto mengambil 1 kelereng di kelompok 1.
Di sini, seharusnya kamu tahu apa yang harus Budi lakukan. Ambil 2 kelereng di kelompok 2 sehingga hanya menyisakan 1 kelereng.
Karena hanya tersisa 1 kelereng, maka dengan terpaksa Anto mengambilnya, maka Anto pun kalah.. (Sebetulnya, kekalahan Anto dimulai sejak awal)

=========================================================================

== CLOSING ==

Semoga simulasi di atas dapat memperjelas.. ^^
*) Dan, ingat, harus selalu mengusahakan pola kalah itu di setiap giliran. Jangan beri kesempatan pada musuh.!! :P (kejamnya..)

*) Tambahan: jangan beritahukan rahasia ini kepada temanmu, kecuali kalau kamu bersedia untuk kalah... Tentunya, tidak seru bukan, kalau semua orang tahu rahasia ini..?? :P

*) N, jika peraturannya diubah: jika yang menang adalah pemain yang mengambil kelereng terakhir, maka pola kalah di atas tetap berlaku kecuali yang nomor (1).. Jadi, bukan kumpulan ganjil dari 1 (1 atau 1-1 atau 1-1-1, dst), tapi kumpulan genap dari 1 (1-1, atau 1-1-1-1, dan seterusnya..)

So, selamat bermain..!!

N, karena hari ini adalah hari Natal, so: Merry Christmas..!! ^^
Click Here to Read More..

Makanan Otak ...(vb) {Jawaban Limit}

Ini adalah lanjutan dari post "Makanan Otak...(v) {Limit}".. Di sini, akan kuberi tahu jawaban dari 20 nomor di post itu. Namun, ada baiknya jika kalian mencoba dulu dengan usaha kalian terlebih dahulu, barulah melirik jawaban di sini untuk dicocokkan.. ^^.. Oh iya, di sini juga ada materi sekilas tentang limit, namun di sini tidak selengkap yang ada di buku text book kalian.. Namanya juga *sekilas*.. XD.

=========================================================================

--Sekilas Tentang Limit--

Sebelum melangkah lebih jauh, ada baiknya kita mengulang materi limit (yang tidak sempat kubuat materinya di blog ini...). Limit adalah suatu pendekatan. Dapat dikerjakan dengan cara memasukkan nilai pendekatan itu langsung ke fungsinya.
Misalnya: .
Namun, tidak selalu cara itu berhasil karena fungsi di titik itu tidak kontinu. Atau dengan kata lain tidak tersambung. Maka, tidak dapat terdefinisikan.
Misalnya: . Jika nilai x langsung dimasukkan ke fungsinya, maka akan terbentuk , yang artinya tidak dapat didefinisikan. Jadi, kita harus mengubah bentuk tersebut menjadi lebih sederhana. (Lihat contoh-contoh soal di bawah). dan juga merupakan bentuk yang tidak dapat didefinisikan.. ^^

Tak lupa, ada juga rumus limit untuk trigonometri untuk x mendekati nol.

Beberapa limit akan menuju nilai yang spesifik. Berikut adalah limit yang merupakan identitas euler.

Eh, ada yang kelupaan lagi, tapi ini lumayan penting.. Suatu fungsi itu punya limit di suatu titik apabila limit kirinya sama dengan limit kanannya.. Apa itu limit kiri? Apa itu limit kanan? Lihat penjelasan di bawah.
Contoh limit kanan:
Contoh limit kiri:
Perhatikan di atas. Limit kiri dan limit kanan di titik itu sama. Jadi, fungsi itu punya limit di x=2.
Aku beri contoh.. , sedangkan. Karena limit kiri dan limit kanan berbeda nilainya, maka tidak dapat didefinisikan. Contoh lain seperti: , sedangkan. Karena nilainya berbeda, maka tidak dapat didefinisikan.

Untuk mencari nilai limit, kita juga dapat menggunakan dalil L' Hospital:

Dalil L' Hospital hanya berlaku jika membentuk atau .

Ternyata, ada cara lain untuk mencari limit fungsi, selain yang sudah disebutkan di atas, yaitu menggunakan metode numerik (biasanya di komputer..). Dan ini juga ampuh untuk fungsi-fungsi yang susah banget disederhanakan dan dikutak-katik. Namun, kerugiannya, menimbulkan error yang relatif besar juga, tergantung seberapa akurat nilai yang kita gunakan.. Langsung ke contoh.
Tentukan nilai .
Maka, kita masukkan saja nilai x yang mendekati nol. Misalkan x=0,000001. Dengan demikian:

(Untuk kasus di atas, akan lebih baik jika kita mencoret variabel x saja, maka kita akan mendapatkan nilai limitnya nol.. Namun, ada beberapa kasus di mana metode numerik sangat berperan.. :D)

=========================================================================

--Here are the answers--
--> Makanan Otak...(v) {Limit} <--

1.	Mudah dikerjakan. Hanya kita coba untuk faktorkan, kemudian, dicoret.. ^^ ________________ ________________ ________________ ***********************************************************************************
2.	Hmm.. Remember that bentuk akar sebaiknya kita kalikan dengan sekawannya.. :D ____________________ ____________________ ____________________ ____________________ ***********************************************************************************
3.	Mulanya memang agak susah, namun kita bisa menyederhanakan dengan mengeluarkan akar x-nya. Coret saja langsung akar x-nya.. :D ***********************************************************************************
4.	_______________________ _______________________ _______________________ _______________________ ***********************************************************************************
5._	Bentuk cos bisa ditransformasikan ke sin gak yach... Yupp.. . _____________ _____________ _____________ _____________

___***********************************************************************************

6.	_____________________ _____________________ _____________________ ***********************************************************************************
7.	_____________ _____________ ***********************************************************************************
8.	Yang satu ini sedikit tricky.. Lihat bahwa __++_________________ _____________________ _____________________ ***********************************************************************************
9.	Lagi-lagi, kalikan dengan sekawan. Lalu, kita bagi pembilang dan penyebut dengan x pangkat tertinggi yang ada di fungsi. Di soal ini, pangkat tertingginya adalah 1, jadi, kita bagi pembilang dan penyebut dengan x. Piece of Cake.. ^^ ___________________________ ___________________________ ___________________________ ***********************************************************************************
10.	Masihkan dikau ingat dengan rumus penjumlahan 2 sudut sinus dengan cosinus?? ^^ _______________ _______________ _______________ ***********************************************************************************
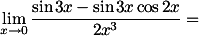
11.	Nah, ingatkah kamu kalau . Selanjutnya, bentuk ini menjadi sangat mudah dikerjakan. ______________________ ______________________ ______________________ ***********************************************************************************
12.	Karena jika nilai x dimasukkan sudah terdefinisi, maka soal ini langsung bisa dikerjakan dengan substitusi. Duh, ini sebetulnya salah nulis soal sich. Sebetulnya bukan + 1 tapi minus 1.. hohoho. Koreksi Soal: Tentukan nilai . = ______________= ______________= ______________= (wew, ternyata mudah..) ***********************************************************************************
13.	Tinggal samakan penyebut.. Lagi-lagi, soal ini sangatlah mudah. ___________________ ___________________ ___________________ ***********************************************************************************
14.	Semudah mensubstitusi nilai x.. ^^. Karena, caranya memang demikian.. ^^ ***********************************************************************************
15.	Selain dengan pemfaktoran, pake dalil L' Hospital juga bisa.. ^^ ***********************************************************************************
16.	bentuk di atas dapat disusun ulang menjadi: ____________ ____________ ____________ Actually, sebenarnya ini aku salah tulis soal *lagi*, yang bener tuh bukan , tapi seharusnya begini: .. Koreksi Soal: Tentukan nilai Bentuk di atas dapat disusun ulang menjadi: Kemudian, kita kerjakan biasa seperti di nomor 9. Namun, kita juga bisa memakai rumus *cepat* yang diturunkan dari penjabaran biasa: == ***********************************************************************************
17.	Perhatikan bentuk yang aneh ini.. Kita bisa men*transformasikan* nilai x yang mendekati tak hingga menjadi y mendekati nol. ________ ________ Maka, bentuk persamaan di atas menjadi: ***********************************************************************************
18.	Ini memakai konsep euler. Jika masih belum jelas, skip dulu soal ini. Lihat nomor 19. = _______________________= _______________________= _______________________= Kita tentukan nilai dari == = = 0. (atau bisa juga gunakan dalil L'Hospital) _______________________= _______________________= 1 Jadi, 1. ***********************************************************************************
19.	= Perhatikan rumus identitas euler: Maka, untuk mengerjakan soal ini, kita harus berusaha membuat bentuk seperti itu. ***********************************************************************************
20.	Wah, sepertinya ini adalah makanan lezat bagi penggemar dalil L' Hospital.. ^^ __________ __________ Note: bisa juga menggunakan cara lain dengan memisalkan . Maka: Maka: _______________ _______________ _______________ _______________ _______________

=========================================================================
Bagaimana? Apakah kalian bisa mengerjakan 20 nomor di atas dengan *sempurna*?? ^^
Btw, aku mohon maap apabila penjelasan di blog ini kurang jelas (coz, banyak cara yang di-skip juga sih..) .. Silakan kalo mo nanya, bagi yang belum mengerti.. ^^
Click Here to Read More..