Mungkin, kalian pernah menemukan soal seperti ini di buku SMA:


Tentukan nilai

Kali ini soal yang diajukan sedikit berbeda. Hanya menambahkan 1 variabel, yaitu sbb:




Tentukan nilai
 .
.PENYELESAIAN
Untuk soal yang pertama:


Tentukan nilai
Jawab:


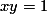






Tentukan nilai



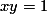




Jika konsep dua variabel sudah dipahami, maka untuk 3 variabel juga sama, namun sungguh lebih ribet... X(. Silakan lihat di bawah...
Soal Kedua:




Tentukan nilai .
.
Jawab:








_____________




_____________
_____________

_____________
_____________
_____________







Tentukan nilai
 .
.







_____________





_____________

_____________


_____________

_____________

_____________




Soal diberikan oleh Simon Lim melalui email. Thx to Simon. :). Penyelesaiannya sudah dibuat:)

trus kalo gitu bisa nyari nilai x, y, ama z gak???
ReplyDeletekalo bisa gimana caranya?
Nilai x, y, dan z saling berotasi. Nilainya ada, namun hampir mustahil untuk bisa dicari dengan aljabar.
ReplyDeleteGunakan metode Gauss Siedel (metode numerik) untuk menemukan nilai x, y, dan z.
Ribed Banget Sih, Enakan Pake Cara Persamaan X pangkat 3 dengan persamaan abcd. jadi nilai X,Y,&Z lebih simpel dengan X.Y.Z=6 maka kemungkinan menemukan nilai X,Y,&Z lebih mudah, dan soalnya lebih gampang diselesaikan...
ReplyDeletedari dulu wa gag pernah paham, apakah hubungannya,
ReplyDeletex,y, dan z dikehidupan nyata???
dari sma disuruh ngitung, pas ud kerja kayaknya gag pernah dipake rumus2 kaya gitu??
mungkin yang jenius aja kali ya yg pake :D
mau nanya dong, itu 10/3, 4/3 sama 8/3 dari mana ya? kok saya dapetnya hasilnya 194
ReplyDelete@anonymous: Nilai x, y, dan z itu bukan bilangan bulat. Jadi, gak bisa dicari coba-coba, meskipun hasil perkaliannya sudah didapat.
ReplyDelete@Yoga: 10/3, 4/3 sama 8/3 sebetulnya didapat dengan eliminasi. Seandainya dikalikan, maka persamaan itu jadi seperti persamaan yang di atas.
194 dari mana ya? 0_o
tolong tampilkan juga contoh-contoh soal serta penyelesaian dari grup dalam struktur aljabar
ReplyDeletetolong tampilkan pembuktian teorema-teorema grup dari struktur aljabar
ReplyDeletecara dapetin nilax x,y dan z-nya bisa ko. ini soal lomba mtk smp tahun 2009 babak final, dan ini soal pembunuh saya. setelah membedah kasus selama berbulan bulan ketemu deh caranya.
ReplyDeletecaranya:
itung panjang di atas sehingga dapet nilai
xy+xz+yz=1
xyz=-6
x+y+z= 4
dari persamaan di atas jadiin persamaan polinom.
x^3-(x+y+z)x^2+(xy+xz+yz)x-(xyz)=0 (kata org persamaan vieta, tapi ga tau deh)
x^3-4x^2+x+6=0
(x+1)(x-2)(x-3)=0
x=-1 V x= 2 V x=3
NO.1 NILAI X AMA Y BRAPA?????
ReplyDeletesaiiaaa sukakk yg beginian...
ReplyDeleteizin posting ulang ea mass...
ini sih seperti soal-soal olimpiade ya, harus mantap dulu materi - materi dasarnya , tanpa itu sulit mencerna cara diatas.
ReplyDeleteSitus Agen Judi Online daftar judi bola terbaik judi poker slot terbaik dan terpercaya 2020
ReplyDeleteSitus Daftar Judi Onlin
Judi Bola Online
Agen judi Bola Terpercaya
Agen Judi Online Resmi