Chinese Remainder Theorem Eksplisit

Di post sebelumnya sudah dibahas mengenai Chinese Remainder Theorem, tapi hanya dijelaskan solusi yang dilakukan secara iteratif. (Lihat di SINI) . Di post ini, akan ditunjukkan Rumus/ Teorema Chinese Remainder Theorem yang eksplisit yang dapat secara langsung digunakan untuk mencari solusi.

Diberikan sistem kongruensi sebagai berikut.

haruslah saling relatif prima
Dengan demikian, kita dapat mencari nilai dengan rumus berikut.

dimana

untuk setiap .
dan adalah invers dari modulo untuk setiap .

Untuk lebih memahami, silakan lihat contoh di bawah. :)

CONTOH 1:
Suatu bilangan bulat positif akan bersisa 1 jika dibagi 3, bersisa 2 jika dibagi 5, dan bersisa 3 jika dibagi 7. Tentukan bilangan bulat terkecil yang memenuhi kondisi tersebut.

Jawab
Soal di atas dapat ditulis ulang menjadi:

Karena 3,5, dan 7 relatif prima, maka rumus CRT (Chinese Remainder Theorem) dapat langsung digunakan.
Kita dapatkan , , , dan . Untuk menentukan , kita selesaikan , menjadi , maka . Untuk menentukan , kita selesaikan , maka . Untuk menentukan , kita selesaikan , maka

Tinggal memasukkan semua elemen yang ada ke dalam rumus.

Jadi, bilangan bulat positif terkecil itu adalah 52. Bisa dicek bahwa 52 akan bersisa 1 jika dibagi3, bersisa 2 jika dibagi 5 dan bersisa 3 jika dibagi 7.

Untuk membuktikan formula ini sangat sederhana. Lihat kotak dibawah.

Tentukan

Solusi yang diberikan adalah

Mula-mula pandang bahwa

(merupakan solusi yang sudah didefinisikan sebelumnya)

Jika solusi tersebut memenuhi syarat awal bahwa akan bersisa jika dibagi untuk setiap , maka solusi tersebut terbukti kebenarannya.

Kita coba periksa sisanya jika dibagi dengan
Karena , maka tentunya .
Karena , mak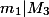a juga.
Dan seterusnya dari hingga
Oleh karenanya:

Menurut definisi sebelumnya , maka

Ternyata, jika dibagi dengan akan bersisa . Artinya, ini sesuai dengan salah satu syarat yang diberikan.

Pembuktian masih dilanjutkan dengan mengecek sisanya jika dibagi .
Karena , maka
Karena , maka .
Dan hal sama juga berlaku pada hingga (silakan dicek sendiri, dan ketahuilah mengapa demikian)
Oleh karenanya:

Karena kita tahu bahwa , maka

Ternyata sesuai dengan syarat baris kedua.

Pembuktian dilanjutkan dengan mengecek sisanya jika dibagi hingga 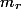. Masing-masing akan menyisakan , hingga . Dengan demikian, definisi awal yang diberikan terbukti.

TERBUKTI sebagai solusi CRT

Namun, ada hal yang masih perlu dibuktikan. Karena mempunyai banyak jawab, akibatnya juga mempunyai banyak jawab.
Misalkan dan adalah solusi CRT yang nilainya berbeda, maka:
________Untuk setiap :

Menggabungkan keduanya:

Sesuai dengan teorema keterbagian bahwa: "jika dan , maka ", maka

Dari hasil di atas, diketahui bahwa antara solusi yang satu dengan solusi yang lain adalah kongruen modulo M. Jadi, solusi CRT menjadi:

TERBUKTI

Untuk lebih memahami penggunaan CRT. Perhatikan contoh di bawah. Kerjakan sebagai latihan.

CONTOH 2:
Temukan integer yang bersisa 1 jika dibagi 2 dan jika dibagi 3

Jawab:


, ,
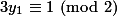, maka
, maka

CONTOH 3:
Temukan integer terkecil yang memenuhi

Jawab:
(Note: akan lebih mudah jika diselesaikan dengan komputer :D)







Kemudian, carilah .
, maka , maka
, maka
, maka , maka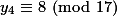
, maka , maka
, maka , maka
(Note: untuk mencari invers modulo, biasakan untuk menggunakan teorema Euler).

Selanjutnya tinggal memasukkan ke rumus

Jadi, bilangan terkecil itu adalah 150999.

=======================================================================

Demikianlah posting kali ini.
Materi CRT memang jarang digunakan dalam olimpiade matematika, namun aplikasinya menarik :D.

Untuk memahaminya, pelajari materi dasar dahulu seperti keterbagian, modulo, dan invers modulo. Jika masih belum paham, tanyakan di comment atau YM atau email, bagian mana yang membuat kamu tidak paham. Key? :).