Everything About Math: Garis-Garis Istimewa Segitiga...(i)

Thursday, October 2, 2008

Garis-Garis Istimewa Segitiga...(i)

Posted by hendry_dext

Huaammmm.... Tugas Berat kuliah akhirnya selese juga. Tapiii, sayangnya, masih banyak tugas menanti.. Hikshikshiks.. ... Tapi, tenang, aku masih sempet-sempetin diri untuk berusaha memberikan ilmu... hwahwahwa.. Kali ini tentang garis-garis istimewa pada segitiga (tapi masih tahap dasar atau setara dengan SMP dan sebaiknya baca juga tentang dalil Stewart).. Tahukah km apa saja garis-garis istimewa itu?

_____1. garis tinggi (altitude)
_____2. garis berat (median)
_____3. garis bagi (angle bisector)
_____4. garis sumbu (perpendicular bisector)

=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=
Garis Tinggi
Garis Tinggi adalah garis yang tegak lurus dari salah satu titik sudut segitiga terhadap sisi yang di depannya.

Perhatikan segitiga ABC. Dari gambar di atas, CD merupakan garis tinggi dengan alasnya adalah garis AB. Namun, titik D tidak selalu berada pada garis AB. Bisa saja terletak pada perpanjangan AB, seperti pada segitiga tumpul (obtuse), seperti pada gambar di bawah

Di atas, diperlihatkan garis tinggi yang berasal dari sudut C. Jika ketiga garis tersebut ditarik dari ketiga sudut, maka ketiga garis tersebut akan berpotongan pada suatu titik (titik itu disebut ortocenter).

Dari gambar di atas, titik T adalah titik ortosenter. Titik ortocenter akan selalu berada di dalam segitiga apabila segitiga itu lancip (acute). Sebaliknya, akan berada di luar, apabila segitiga itu tumpul (obtuse). Kalau segitiga siku-siku (right triangle), tentunya ortocenter akan berada di titik sudut siku-sikunya... Hmmm..

Panjang garis tinggi dapat dihitung dengan mengetahui Luas segitiga. Lalu, dengan memakai rumus Luas = 1/2.a. t, maka tentunya tinggi segitiga (t) bisa diketahui dengan mudah. Cara lain bisa dengan mengetahui panjang proyeksinya terlebih dahulu, lalu menggunakan phytagoras untuk mendapatkan tingginya... (Lihat dalil Stewart)^^..

Contoh soal 1: Perhatikan segitiga ABC di bawah. Diketahui AB=20 cm. BC = 24 cm. AD = 16 cm. Htunglah tinggi CE!

Jawab:
Luas segitiga dengan alas BC = Luas segitiga dengan alas AB
$\frac{1}{2}.BC.AD = \frac{1}{2}.AB.CE$
24.16 = 20.CE
CE = 19,2 cm.

Wah, mudahhh sekalleeee.... Wew... Memank sih mudah.. Namanya juga soal SMP.. =.="

=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=
Garis Berat
Garis berat adalah garis yang terhubung dari titik sudut suatu segitiga ke titik tengah sisi yang berlawanan. Hal ini mengakibatkan daerah yang terbagi oleh garis berat menjadi sama luasnya. Lihat gambar di bawah.. Luas segitiga ACD akan sama dengan BCD karena panjang alas dan tingginya sama.

Ketiga garis berat akan berpotongan di satu titik, yang namanya centroid/center of gravity/titik pusat massa. Di titik inilah benda tersebut dapat setimbang.

Garis berat memiliki keistimewaan: garis berat-garis berat sebuah segitiga selalu saling berpotongan menurut perbandingan 2:1.
Lihat contoh gambar di atas. Maka, CT:TF = AT:TD = BT:ET = 2:1.

Panjang garis berat dapat dicari menggunakan dalil Stewart.
Ambil contoh gambar di atas, maka panjang CF dicari dengan cara berikut:

===>rumus panjang garis berat.

Contoh Soal 2:
Pada segitiga ABC, CD merupakan garis berat. AB=14 cm, BC =10 cm dan AC=6cm. Hitung panjang CD!

Jawab:

=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=
Garis Bagi Dalam Segitiga
Garis bagi dalam adalah garis yang melalui titik sudut segitiga dan membagi kedua sudut di sebelahnya sama besar. Garis ini terletak dalam segitiga.

Garis bagi juga memiliki keistimewaan. Lihat gambar di atas. c_1

= b:a. Perbandingan ini selalu berlaku untuk garis bagi dalam. Selain itu, perbandingan c_1

: (

) = b: (b+a) juga berlaku.

Garis bagi dalam ini berpotongan di satu titik (namanya incenter), dan titik ini merupakan pusat dari lingkaran dalam segitiga (incircle). Lihat gambar di bawah. Jari-jarinya dapat dicari dengan menggunakan prinsip Luas segitiga = Luas 3 segitiga dalam.

Lalu, bagaimana cara kita tahu berapa panjang garis bagi segitiga?? Lihat gambar di bawah. Pertama, kita harus mencari panjang

dan

. Kemudian, gunakan dalil Stewart. Ulasan lengkapnya ada di bawah.

Perhatikan gambar di samping!
CD =

disebut garis bagi dalam $\angle$ C.
$\angle$ ACD = $\angle$ DCB.
Berlaku: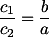

Karena

= c, maka:

===>

Dengan menggunakan dalil Stewart, maka didapat:

Contoh Soal 3:
Pada suatu segitiga ABC, diketahui a=6cm, b=12 cm, dan c=4 cm. Hitunglah panjang garis bagi dalam titik C(CD)!

Jawab:

===>

=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=
Garis Bagi Luar Segitiga
Merupakan garis yang berasal dari titik sudut segitiga yang membagi dua sudut yang sama antara suatu sisi segitiga dengan perpanjangan sisi yang lain. Garis ini terletak di luar segitiga.

Maka, perbandingan yang selalu terjadi ialah:

= b:a.

Panjang garis bagi luar segitiga dapat dihitung dengan cara berikut.
Anggap b>a,

= c, maka:
$c_1 = \frac{b}{b-a} \times c$ ===>

===>

Maka, dengan menggunakan dalil Stewart, didapat:

=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=
Garis sumbu
Garis sumbu adalah garis yang melalui titik tengah suatu sisi segitiga dan tegak lurus terhadap sisi itu. Ketiga garis sumbu bertemu di satu titik yang dinamakan circumcenter. titik tersebut merupakan pusat lingkaran luar segitiga (circumcircle). Jari-jari lingkaran ini dapat dicari menggunakan prinsip kesebangunan segitiga.

=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=
SOAL TANTANGAN (gabungan materi dalil Stewart)
Silakan jawab di comment dengan cara singkat. Jika jawaban benar, saya akan menambahkan jawaban lengkap di halaman ini. Note: soal di sini masih tergolong mudah. Masih banyak soal yang lebih rumit dan variatif. ^^

1. Dalam segitiga PQR panjang sisi PQ = 16 cm, QR=9 cm, dan PR=19 cm. Hitunglah luas segitiga PQR! Hitung garis tinggi dari titik P(PS), Q(QT), dan R(RU)!

2. Sebuah segitiga ABC dengan AB = 8 cm, BC = 9cm, dan AC = 7cm. Garis tinggi AD dan BE berpotongan di titik T. Berapakah perbandingan panjang AT:TD ?

3. Sebuah segitiga ABC dengan AB=5 cm, BC = 6 cm, dan AC = 7 cm. AD dan BE adalah garis tinggi. Hitunglah luas segitiga CDE!

4. Dalam segitiga ABC, panjang sisi AB = 4 cm, BC = 7cm, dan AC = 8cm. Garis berat-garis berat AD,BE, dan CF saling berpotongan di titik Z. Hitunglah panjang AD, BZ, ZF!

5. Diketahui ada sebuah trapesium. Sisi-sisi sejajar trapesium adalah 16 cm dan 10 cm. Panjang kaki-kakinya 8 cm dan 10 cm. Hitunglah panjang kedua diagonalnya!

6. Diketahui segitiga ABC, AB=6 cm, AC = 7 cm, dan BC = 8cm. D pada AC dengan CD=3cm, E pada BC dengan CE = 5cm. Hitunglah panjang DE!

7. Diketahui segitiga ABC siku-siku di C. AC = 12 cm dan BC = 16 cm. Titik D dan E berada di ruas garis AB dimana AD = DE = EB. Hitunglah panjang CD dan CE!

8. Pada sebuah segitiga ABC, diketahui AB = 8 cm, BC = 7 cm, dan AC = 6cm. Pada perpanjangan AB terdapat titik D, sehingga BD = 1/2 AD. Hitunglah panjang CD!

9. Diketahui sebuah segitiga ABC dengan AC = 8cm, AB = 6cm dan BC = 12 cm. Titik D pada AB dan titik E pada BC sehingga AD:AB = 1:3 dan BE = CE. Hitunglah panjang DE!

10. Sisi-sisi sejajar sebuah trapesium 6 cm dan 36 cm. Panjang diagonalnya 21 cm dan 27 cm. Hitunglah panjang kaki-kaki trapesium tersebut!

11. Sebuah segitiga ABC dengan AB = 10 cm, BC = 13 cm, dan AC = 17 cm. Titik P pada perpanjangan AB sehingga AP:PB = 7:5. Hitunglah panjang CP!

12. Suatu trapesium dengan sisi-sisi sejajar 12 cm dan 25 cm. Panjang kaki-kakinya 12 cm dan 14 cm. Hitunglah luas trapesium tersebut!

13. Sisi-sisi sejajar sebuah trapesium 16 cm dan 5 cm. Panjang kaki-kakinya 6 cm dan 7 cm. Hitunglah panjang garis yang menghubungkan titik tengah dari sisi-sisi sejajarnya.

14. Sebuah segitiga ABC siku-siku di A. AB=6 cm, dan AC=8 cm. AD adalah garis bagi dalam. Hitunglah panjang BD, CD, dan AD!

15. Sebuah segitiga ABC dengan AB = 21 cm, BC = 18 cm, dan AC = 12 cm. CD adalah garis bagi. E adalah titik tengah BC. Hitunglah panjang DE!