Di post sebelumnya, kita belajar mengenai algoritma simpleks, namun persamaan linearnya haruslah STANDAR. Ciri-ciri standar adalah sbb:
1. Fungsi objektifnya maksimum (optional)
2. Semua variabelnya bernilai positif.
3. Semua RHS dari kendala bernilai positif.
4. Semua kendalanya harus berlambang
.
1. Fungsi objektifnya maksimum (optional)
2. Semua variabelnya bernilai positif.
3. Semua RHS dari kendala bernilai positif.
4. Semua kendalanya harus berlambang
.Jika tidak standar, maka kita harus mengubahnya ke standar terlebih dahulu, kemudian kita menggunakan langkah 6 tahap seperti yang sudah kita pelajari sebelumnya.. Agar lebih mengerti, kita lihat saja contoh di bawah. :)
Fungsi Objektif adalah Minimum
Kalau fungsi objektifnya minimum, maka ada 2 alternatif cara yang dapat kita gunakan:
| 1. | Kalikan kedua ruas dengan minus. Sekarang, fungsi sudah berubah menjadi maksimum. ATAU |
| 2. | Masukkan ke dalam tabel awal Simpleks seperti biasa. Sekarang, pemilihan kolom kunci didasarkan pada angka yang positif terbesar. |
Andaikan sekarang kamu adalah karakter utama dalam game RPG. Sekarang kamu akan menghadapi suatu boss. Boss ini hanya menggunakan 1 skill, yaitu "charge". Dengan menggunakan skill ini, sang boss tidak akan menyerang kamu sebanyak 50 giliran, namun setelah giliran yang ke-50, dia akan menghabisi 100% HP (Hit Points)-mu
Nah, setiap giliran, kamu hanya bisa menyerang boss dengan menggunakan salah satu dari 3 jurus yang ada: jurus api, air, dan angin. Dengan menggunakan jurus api, HP boss akan berkurang 1%, MP (Magic Points) kamu akan bertambah sebesar 5, namun HP kamu akan berkurang sebesar 2%. Jurus air lebih hebat dari jurus api, karena dia akan mengurangi 2% HP boss dan menambah HP-mu sebesar 3%, namun MP yang digunakan untuk jurus air adalah 10. Jurus angin lebih hebat lagi daripada jurus api karena jurus ini mampu mengurangi 3% HP boss, namun MP yang digunakan sebesar 25, dan akan mengurangi 1% HP-mu. (Note: % di sini adalah persen dari total.)
Andaikan kamu melawan boss dalam keadaan awal HP full dan jumlah MP sebesar 380, maka apakah boss itu dapat kamu kalahkan?
Andaikan kamu melawan boss dalam keadaan awal HP full dan jumlah MP sebesar 380, maka apakah boss itu dapat kamu kalahkan?
JAWAB CARA I: MENGUBAH FUNGSI MIN menjadi MAX
Mungkin pada awalnya kalian merasa kebingungan, bagaimana merumuskan persamaan linear untuk kasus di atas. Namun, sesungguhnya cukup mudah. Ingat bahwa tujuan kita hanya satu, yaitu mengalahkan boss. Agar boss kalah, maka HPnya menjadi nol. Maka, fungsi objektifnya adalah meminimumkan HP boss..
Misalkan:
= HP boss yang masih ada.
= banyaknya jurus api yang digunakan
= banyaknya jurus air yang digunakan
= banyaknya jurus angin yang digunakan.
Maka Rumusan kasus di atas adalah sbb:
Untuk kendala yang kedua, kamu dapat menyederhanakannya:
Lalu, tambahkan ketiga kendala dengan variabel slack..
Sesudah itu, ubahlah fungsi objektif Z min menjadi Z maks, dengan mengalikan kedua ruas fungsi objektif dengan minus 1.
Kemudian, pindahkan semua variabel ke ruas kiri, dan tinggalkan konstantanya di ruas kanan, maka menjadi: 
. (Note: konstanta untuk fungsi objektif boleh negatif)
Maka, rumusan kasus di atas menjadi sbb:
Tabel awal simpleksnya:
Sebagai catatan: kolom Z tidak akan dipilih sebagai kolom kunci. Akibatnya kolom Z tidak akan berubah sampai akhir iterasi...
Selanjutnya, pengerjaan sama seperti langkah 6 tahap sebelumnya...
Hasil iterasi 1:
Hasil iterasi 2:
Kondisi optimum sudah terpenuhi..
Solusinya adalah:
Banyaknya jurus api =
Banyaknya jurus air =
Banyaknya jurus udara =
.. Jika dikalikan minus 1, maka hasilnya 
. Maka, sisa HP boss yang minimum adalah 8. Karena tidak mencapai nol, maka boss tidak dapat dikalahkan dalam kasus ini.
Misalkan:
= HP boss yang masih ada. = banyaknya jurus api yang digunakan = banyaknya jurus air yang digunakan = banyaknya jurus angin yang digunakan.Maka Rumusan kasus di atas adalah sbb:
Fungsi Objektif:
Kendala:
Kendala variabel:
dibagi 5, maka hasilnya:
Lalu, tambahkan ketiga kendala dengan variabel slack..
Sesudah itu, ubahlah fungsi objektif Z min menjadi Z maks, dengan mengalikan kedua ruas fungsi objektif dengan minus 1.
kalikan minus 1, maka hasilnya:
. (Note: konstanta untuk fungsi objektif boleh negatif)Maka, rumusan kasus di atas menjadi sbb:
Fungsi Objektif:
Kendala:
Kendala variabel:
Selanjutnya, pengerjaan sama seperti langkah 6 tahap sebelumnya...
Hasil iterasi 1:
Solusinya adalah:
Banyaknya jurus api =
Banyaknya jurus air =
Banyaknya jurus udara =
.. Jika dikalikan minus 1, maka hasilnya . Maka, sisa HP boss yang minimum adalah 8. Karena tidak mencapai nol, maka boss tidak dapat dikalahkan dalam kasus ini.JAWAB CARA II: FUNGSI MIN TIDAK DIUBAH, TAPI PEMILIHAN KUNCI DIDASARKAN PADA ANGKA POSITIF TERBESAR.
Persamaan matematika yang kita rumuskan tidak berbeda jauh dengan cara I.. Bedanya, pada fungsi objektif, biarkan Z adalah fungsi minimum..
Dengan hanya meng-copy dari sebelumnya, kita dapatkan rumusan sbb:
Kita langsung saja buat tabel awal simpleksnya... :)
Pemilihan kolom kunci sekarang dipilih menurut angka di baris Z yang positif dan terbesar. Maka, langsung kita akan dapatkan hasil sbb:
Hasil iterasi 1:
Hasil iterasi 2:
Ternyata, cara II maupun cara I menghasilkan jawaban yang persis sama. Bahkan perhitungannya pun sebetulnya sama.. Hanya beda tanda negatif di baris Z.. :)
Dengan hanya meng-copy dari sebelumnya, kita dapatkan rumusan sbb:
Fungsi Objektif:
Kendala:
Kendala variabel:
Hasil iterasi 1:
Note: Dijelaskan di post sebelumnya bahwa SIMPLEKS STANDAR harus memiliki fungsi objektif yang maksimum. Sebenarnya, pernyataan ini bersifat OPTIONAL.. Di beberapa buku text lain, baik jenis maksimum maupun jenis minimum keduanya dianggap bentuk standar, karena keduanya bekerja secara unik. Sekali lagi, ini tergantung dari sisi mana pembaca melihatnya. :)
Variabel Berkendala
Di contoh-contoh di atas, kita selalu berurusan dengan variabel positif... Kenapa positif? Karena biasanya tidak ada produk yang negatif. Misalnya, pabrik yang memproduksi kursi, pasti berproduksi positif dan bukan negatif... Tapi, bagaimana jika hal-hal yang tidak biasanya terjadi?
Untuk variabel berkendala, sebaiknya, variabelnya dimodif sehingga menjadi "
". Cara memodifikasinya adalah sbb:
". Cara memodifikasinya adalah sbb:| 1. | Jika ada kendala , maka definisikan kembali  dimana  |
| 2. | Jika ada kendala , maka definisikan kembali dimana |
| 3 | Jika ada kendala , maka definisikan kembali dimana |
| 4. | Jika variabel tidak dibatasi, maka definisikan kembali dimana  |
Tentukan solusi optimal untuk fungsi
dengan kendala:
, 
Karena , maka definisikan 
dimana 
. Dengan adanya definisi tersebut, maka kita juga harus mensubstitusi semua variabel 
menjadi 
.
Maka rumusannya menjadi:
Tidak lupa semua kendala diberi variabel slack, maka rumusannya sekarang menjadi sbb:
Bentuk di atas sudah merupakan SIMPLEKS STANDAR.. Kalian tinggal meneruskannya dengan langkah 6 tahap...
Hasil akhir iterasi ke2:
Solusinya:
, maka definisikan dimana . Dengan adanya definisi tersebut, maka kita juga harus mensubstitusi semua variabel menjadi .Maka rumusannya menjadi:
Fungsi Objektif:
Kendala:
Kendala variabel:
Keterangan tambahan:
Fungsi Objektif:
Kendala:
Kendala variabel:
Keterangan tambahan:
Hasil akhir iterasi ke2:
Tentukan solusi optimal untuk fungsi
dengan kendala:
, 
Definisikan kembali: 
dan 
maka rumusannya menjadi:
Disederhanakan menjadi:
Selanjutnya, tambahkan variabel Slack pada setiap kendala dan kemudian lanjutkan dengan pembuatan tabel simpleks..
Hasil akhir iterasi 2:
Solusinya:
dan maka rumusannya menjadi:Fungsi Objektif:
Kendala:
Kendala variabel:
Keterangan tambahan:
dan
dan Fungsi Objektif:
Kendala:
Kendala variabel:
Keterangan tambahan:
dan
dan Hasil akhir iterasi 2:
(KENDALA VARIABEL BERLEBIH DAN BERGANDA)Tentukan solusi optimal untuk fungsi
dengan kendala:
, 
, 
, 
, 
, 
JAWAB:
Perhatikan bahwa kendala , , , adalah kendala-kendala yang berlebih... Dari 4 kendala itu, sebenarnya ada 3 yang dapat dihilangkan. (Tahukah kamu, yang mana 3 dari 4 kendala itu yang bisa dihilangkan? Coba kalian berpikir...)
Kemudian, lihat kendala. Kendala ini dapat dipecah menjadi 2 baris kendala, yaitu: 
dan 
.
Maka, rumusan kasus di atas disederhanakan sbb:
Lihat bahwa pada kendala variabel terdapat kendala untuk 
sebanyak 2 baris (berganda). Hal ini tentunya tidak dimungkinkan, karena pemodifikasian hanya dapat dilakukan untuk salah satu saja. Oleh karena itu, pilih salah satu untuk dimodif, dan satunya lagi dipindahkan ke bagian kendala. Di contoh ini, kita akan memodif , maka hasil rumusan sekarang adalah sbb:
Sekarang, kita akan memodifikasi kendala variabelnya. Definisikan:
Kemudian, substitusikan variabel yang ada:
Disederhanakan menjadi:
Oooopss. Ternyata ada RHS pada kendala pertama yang bernilai negatif...
Jawaban soal ini akan dilanjutkan di bagian ketiga di bawah.
, , , adalah kendala-kendala yang berlebih... Dari 4 kendala itu, sebenarnya ada 3 yang dapat dihilangkan. (Tahukah kamu, yang mana 3 dari 4 kendala itu yang bisa dihilangkan? Coba kalian berpikir...)Kemudian, lihat kendala
. Kendala ini dapat dipecah menjadi 2 baris kendala, yaitu: dan .Maka, rumusan kasus di atas disederhanakan sbb:
Fungsi Objektif:
Kendala:
Kendala variabel:
sebanyak 2 baris (berganda). Hal ini tentunya tidak dimungkinkan, karena pemodifikasian hanya dapat dilakukan untuk salah satu saja. Oleh karena itu, pilih salah satu untuk dimodif, dan satunya lagi dipindahkan ke bagian kendala. Di contoh ini, kita akan memodif , maka hasil rumusan sekarang adalah sbb:Fungsi Objektif:
Kendala:
Kendala variabel:
Kemudian, substitusikan variabel yang ada:
Fungsi Objektif:
Kendala:
Kendala variabel:
Keterangan:
Fungsi Objektif:
Kendala:
Kendala variabel:
Keterangan:
Jawaban soal ini akan dilanjutkan di bagian ketiga di bawah.
RHS Kendala Bernilai Negatif
Jika ada kendala yang bernilai negatif, cukup kalikan dengan minus 1.
LANJUTAN JAWABAN CONTOH SOAL 4:
Perhatikan rumusan sebelumnya. Kita menemukan ada kendala yang RHS-nya negatif, yaitu kendala berikut.
Sekarang, rumusannya sekarang menjadi:
Oooopss. Ternyata ada kendala yang lambangnya "
".. Hmmm... Kita belum belajar hal ini, maka kita skip dulu, dan lanjutkan membaca bagian keempat di bawah.
Kalikan minus 1 pada kedua ruas, maka hasilnya:
Fungsi Objektif:
Kendala:
Kendala variabel:
Keterangan:
".. Hmmm... Kita belum belajar hal ini, maka kita skip dulu, dan lanjutkan membaca bagian keempat di bawah.
Kendala Berlambang ≥
Di soal-soal sebelumnya, kita selalu berurusan dengan kendala yang berlambang
. Kendala dengan lambang dapat dengan mudah dijadikan "=" dengan penambahan satu variabel Slack.Sebagai contoh:
dapat diubah menjadi:
dimana
Akan tetapi, untuk kendala yang berlambang
, cara yang sama tidak dapat digunakan. Perhatikan contoh di bawah.
mungkin kalian pikir, kendala di atas bisa diubah menjadi seperti berikut:
dimana (di sini, S disebut sebagai variabel Surplus, bukan Slack)
Kelihatannya sih benar.. Namun, solusi awal simplex selalu dimulai dari titik (0,0). Artinya, ketika 
dan 
, maka 
akan bernilai negatif, sehingga akan melanggar syarat nonnegativitas..
dan , maka akan bernilai negatif, sehingga akan melanggar syarat nonnegativitas..Jadi, bagaimana cara agar syarat nonnegativitas ini tidak dilanggar?
Ans: Salah satu caranya adalah dengan membuat suatu VARIABEL ARTIFICIAL yang berfungsi untuk menampung nilai RHS untuk sementara. Variabel ini untuk selanjutnya harus di-nol-kan, agar variabel Slack dapat memainkan peranannya.
Dengan demikian, yang benar adalah sebagai berikut:
dapat diubah menjadi:
dimana 
DAN 
harus di-nol-kanKita dapat mengecek kebenarannya, dengan memasukkan
dan , maka sekarang akan bernilai nol dan 
.Nah, bagaimana cara kita membuat VARIABEL ARTIFICIAL menjadi nol?
Ans: Di fungsi objektif
tambahkan HAMBATAN variabel ini dengan konstanta yang sangat besar sekali.. Konstanta ini kita beri simbol 
.. (Teknik ini sering disebut dengan teknik M)Sebagai contoh:
| 1. | Jika adalah fungsi maksimum, tambahkan  di ruas yang berlawanan |
| 2. | Jika adalah fungsi minimum, tambahkan  di ruas yang berlawanandimana M adalah bilangan yang sangat besar sekali (bisa kalian anggap sebagai 999999) |
Langsung saja kita ke contoh soal yang sederhana.. :)
Tentukan solusi optimal untuk fungsi
dengan kendala:
JAWAB
Dengan berpedoman pada prinsip di atas, kita dapat langsung merumuskan kasus di atas menjadi sbb:
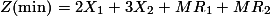
Selanjutnya, kita akan menghilangkan unsur variabel artifisial di fungsi Z, sekaligus memberikan pemecahan awal bagi RHS baris Z.
Kita tahu bahwa:
Dari kendala 1:
Dari kendala 2:
Substitusikan nilai
dan 
ini ke fungsi Z:
disederhanakan menjadi:
Maka, kita mendapatkan rumusan yang baru yaitu sbb:
Kita kerjakan dengan simpleks 6 tahap yang biasanya kita lakukan:
Iterasi 1:
Tabel awal Simpleks:
Jangan bingung dengan simbol M. Anggap saja M itu adalah bilangan yang sangat besar seperti 1000000.. Pengerjaan simpleks kita lakukan dengan langkah-langkah yang sama..
Ingat juga bahwa Z adalah fungsi minimum, artinya pemilihan kolom kunci didasarkan pada angka yang positif terbesar di baris Z.
Hasil iterasi 1:
Hasil iterasi 2:
Tabel sudah optimum karena tidak ada lagi variabel positif di baris Z.
Solusi:
, 
, dan 
Fungsi Objektif:
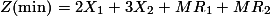
Kendala:
Kendala variabel:
Kita tahu bahwa:
Dari kendala 1:
Dari kendala 2:
Substitusikan nilai
dan ini ke fungsi Z: Pindah ruas:
Fungsi Objektif:
Kendala:
Kendala variabel:
Iterasi 1:
Tabel awal Simpleks:
Ingat juga bahwa Z adalah fungsi minimum, artinya pemilihan kolom kunci didasarkan pada angka yang positif terbesar di baris Z.
Hasil iterasi 1:
Tabel sudah optimum karena tidak ada lagi variabel positif di baris Z.
Solusi:
, , dan 
Tentukan solusi optimal untuk fungsi
dengan kendala:
Soal di atas hanya menggabungkan kendala yang berlambang "" dan berlambang ""..
Kita rumuskan masalah tersebut menjadi sbb:
Dari kendala 3: 
Dari kendala 4:
Substitusikan nilai dan ini ke fungsi Z. Setelah disederhanakan, hasilnya adalah sebagai berikut.
Kita sudah mendapatkan rumusan yang diperbarui:
Lakukan iterasi Simplex
Iterasi 1:
Tabel awal simplex:
Hasil akhir iterasi 1:
Iterasi 2:
Hasil akhir iterasi 2:
Iterasi 3:
Hasil akhir iterasi 3:
Iterasi 4:
Hasil akhir iterasi 4:
Tabel di atas sudah optimal, meskipun masih ada angka negatif pada baris Z di kolom R2.. Mengapa? Karena jika variabel R2 dipilih, maka R2 akan bernilai positif.. Padahal, di kondisi awal, nilai dari variabel artificial (R1 dan R2) haruslah bernilai nol. Artinya, R2 tidak dapat dipilih.. Jadi, kondisi optimal sudah terpenuhi..
Solusi:
, 
, 
dan 
" dan berlambang ""..Kita rumuskan masalah tersebut menjadi sbb:
Fungsi Objektif:
Kendala:
Kendala variabel:
Dari kendala 4:
Substitusikan nilai
dan ini ke fungsi Z. Setelah disederhanakan, hasilnya adalah sebagai berikut.Fungsi Objektif:
Kendala:
Kendala variabel:
Iterasi 1:
Tabel awal simplex:
| Var Basis | Z | X1 | X2 | X3 | S1 | S2 | S3 | R1 | S4 | R2 | RHS |
| Z | 1 | -2M-1 | -M-2 | M-3 | 0 | 0 | M | 0 | M | 0 | -23M |
| S1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 50 |
| S2 | 0 | 0 | 2 | 3 | 0 | 1 | 0 | 0 | 0 | 0 | 23 |
| R1 | 0 | 2 | -1 | 0 | 0 | 0 | -1 | 1 | 0 | 0 | 12 |
| R2 | 0 | 0 | 2 | -1 | 0 | 0 | 0 | 0 | -1 | 1 | 11 |
Hasil akhir iterasi 1:
| Var Basis | Z | X1 | X2 | X3 | S1 | S2 | S3 | R1 | S4 | R2 | RHS |
| Z | 1 | 0 | -2M-2.5 | M-3 | 0 | 0 | -0.5 | M+0.5 | M | 0 | -11M+6 |
| S1 | 0 | 0 | 1.5 | 1 | 1 | 0 | 0.5 | -0.5 | 0 | 0 | 44 |
| S2 | 0 | 0 | 2 | 3 | 0 | 1 | 0 | 0 | 0 | 0 | 23 |
| X1 | 0 | 1 | -0.5 | 0 | 0 | 0 | -0.5 | 0.5 | 0 | 0 | 6 |
| R2 | 0 | 0 | 2 | -1 | 0 | 0 | 0 | 0 | -1 | 1 | 11 |
Iterasi 2:
Hasil akhir iterasi 2:
| Var Basis | Z | X1 | X2 | X3 | S1 | S2 | S3 | R1 | S4 | R2 | RHS |
| Z | 1 | 0 | 0 | -4.25 | 0 | 0 | -0.5 | M+0.5 | -1.25 | M+1.25 | 19.75 |
| S1 | 0 | 0 | 0 | 1.75 | 1 | 0 | 0.5 | -0.5 | 0.75 | -0.75 | 35.75 |
| S2 | 0 | 0 | 0 | 4 | 0 | 1 | 0 | 0 | 1 | -1 | 12 |
| X1 | 0 | 1 | 0 | -0.25 | 0 | 0 | -0.5 | 0.5 | -0.25 | 0.25 | 8.75 |
| X2 | 0 | 0 | 1 | -0.5 | 0 | 0 | 0 | 0 | -0.5 | 0.5 | 5.5 |
Iterasi 3:
Hasil akhir iterasi 3:
| Var Basis | Z | X1 | X2 | X3 | S1 | S2 | S3 | R1 | S4 | R2 | RHS |
| Z | 1 | 0 | 0 | 0 | 0 | 1.0625 | -0.5 | M+0.5 | -0.1875 | 0.1875 | 32.5 |
| S1 | 0 | 0 | 0 | 0 | 1 | -0.4375 | 0.5 | -0.5 | 0.3125 | -0.3125 | 30.5 |
| X3 | 0 | 0 | 0 | 1 | 0 | 0.25 | 0 | 0 | 0.25 | -0.25 | 3 |
| X1 | 0 | 1 | 0 | 0 | 0 | 0.0625 | -0.5 | 0.5 | 0.3125 | 0.1875 | 9.5 |
| X2 | 0 | 0 | 1 | 0 | 0 | 0.125 | 0 | 0 | -0.375 | 0.375 | 7 |
Iterasi 4:
Hasil akhir iterasi 4:
| Var Basis | Z | X1 | X2 | X3 | S1 | S2 | S3 | R1 | S4 | R2 | RHS |
| Z | 1 | 0 | 0 | 0 | 1 | 0.625 | 0 | M | 0.125 | -0.125 | 63 |
| S3 | 0 | 0 | 0 | 0 | 2 | -0.875 | 1 | -1 | 0.625 | -0.625 | 61 |
| X3 | 0 | 0 | 0 | 1 | 0 | 0.25 | 0 | 0 | 0.25 | -0.25 | 3 |
| X1 | 0 | 1 | 0 | 0 | 1 | -0.375 | 0 | 0 | 0.125 | -0.125 | 40 |
| X2 | 0 | 0 | 1 | 0 | 0 | 0.125 | 0 | 0 | -0.375 | 0.375 | 7 |
Tabel di atas sudah optimal, meskipun masih ada angka negatif pada baris Z di kolom R2.. Mengapa? Karena jika variabel R2 dipilih, maka R2 akan bernilai positif.. Padahal, di kondisi awal, nilai dari variabel artificial (R1 dan R2) haruslah bernilai nol. Artinya, R2 tidak dapat dipilih.. Jadi, kondisi optimal sudah terpenuhi..
Solusi:
, , dan Karena Contoh Soal nomor 4 belum selesai dijawab karena ada kendala berlambang "
", maka di bawah akan dilanjutkan penyelesaiannya..LANJUTAN JAWABAN CONTOH SOAL 4:
Terakhir kali kita menemukan adanya kendala , maka kendala ini dapat diberi variabel Surplus dan Artifisial, seperti yang sudah kita pelajari sebelumnya..
Rumusannya diperbarui sbb:
Substitusikan variabel ke fungsi .
Rumusan yang diperbarui adalah sbb:
Masukkan ke tabel Simpleks, namun kali ini kita tidak perlu menyertakan kolom , karena kolom ini tidak akan berubah sepanjang iterasi. Kita juga tidak perlu menyertakan kolom untuk variabel artifisial (), karena setahu saya, kolom ini tidak akan pernah dijadikan kolom kunci. :).
Iterasi 1:
Tabel awal simpleks
Ketika memilih kolom X2' sebagai kolom kunci, kalian akan mempunyai 2 kemungkinan dalam pemilihan baris kunci: antara baris kendala pertama dan baris di kendala kedua, karena kedua-duanya memiliki rasio yang sama (5:1) dan (15:3).. Dalam kasus ini, pilihlah salah satu,. Pilihan manapun tidak mempengaruhi solusi yang ada. :)
Hasil iterasi 1:
Tabel simpleks sudah optimal.
Solusi:
, maka kendala ini dapat diberi variabel Surplus dan Artifisial, seperti yang sudah kita pelajari sebelumnya..Rumusannya diperbarui sbb:
Fungsi Objektif:
Kendala:
Kendala variabel:
Keterangan:
ke fungsi .Rumusan yang diperbarui adalah sbb:
Fungsi Objektif:
Kendala:
Kendala variabel:
Keterangan:
, karena kolom ini tidak akan berubah sepanjang iterasi. Kita juga tidak perlu menyertakan kolom untuk variabel artifisial (), karena setahu saya, kolom ini tidak akan pernah dijadikan kolom kunci. :).Iterasi 1:
Tabel awal simpleks
Ketika memilih kolom X2' sebagai kolom kunci, kalian akan mempunyai 2 kemungkinan dalam pemilihan baris kunci: antara baris kendala pertama dan baris di kendala kedua, karena kedua-duanya memiliki rasio yang sama (5:1) dan (15:3).. Dalam kasus ini, pilihlah salah satu,. Pilihan manapun tidak mempengaruhi solusi yang ada. :)
Hasil iterasi 1:
Tabel simpleks sudah optimal.
Solusi:
Kerjakan soal-soal berikut. :)
Berikut adalah jawaban dari kedua soal di atas:
| 1. | Minimumkan fungsi  dengan batasan:    (Hamdy A Taha book page 111) |
| 2. | Maksimumkan fungsi  dengan batasan:     ,  ,  ,   |
Berikut adalah jawaban dari kedua soal di atas:
| 1. | Berikut adalah tabel awal simpleksnya, namun kolom Z dan kolom untuk R sudah ditiadakan, untuk menghemat penulisan..  ,  , dan  |
| 2. | Rumusan masalahnya adalah sebagai berikut. Fungsi Objektif:  Kendala:  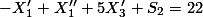   Kendala variabel: Keterangan:    Setelah melakukan 2 kali iterasi, maka tabel sudah optimum, dan hasilnya:  ,  ,  , dan      |
CLOSING
Saya akui, post kali ini memang merupakan post yang sangat berat untuk dibaca. Saya jamin, kalian tidak akan mengerti isi dari post ini jika kalian hanya membacanya sekilas...!! Apalagi kalau lompat-lompat..!!!! Saya sendiri belajar sampai tahap ini butuh waktu kurang lebih 3 minggu kuliah.. Dan, di kuliah sendiri materinya tidak sedalam yang diberikan di post ini..
Untuk mengerti keseluruhan isi post ini, bacalah hingga sedetil mungkin.. Pahami maksudnya. Dan jangan lupha sediakan kertas buram minimal 10 lembar dan juga kalkulator!! Kerjakan setiap contoh yang diberikan. Jika merasa mentok dan otak terasa panas, tinggalkan sejenak baru lanjutkan keesokan harinya.. Jika masih kurang mengerti, silakan tanya saya via YM..
Simpleks merupakan materi yang cukup membuat pusing di awal pelajaran Riset Operasi, namun materi sesudahnya akan berasa lebih mudah, misalnya masalah penugasan, transportasi, dynamic programming..
Jika materi di atas sudah kalian pahami, maka kalian boleh melanjutkan ke tahap berikutnya.. (Post untuk berikutnya sedang dibuat :P)..
Untuk mengerti keseluruhan isi post ini, bacalah hingga sedetil mungkin.. Pahami maksudnya. Dan jangan lupha sediakan kertas buram minimal 10 lembar dan juga kalkulator!! Kerjakan setiap contoh yang diberikan. Jika merasa mentok dan otak terasa panas, tinggalkan sejenak baru lanjutkan keesokan harinya.. Jika masih kurang mengerti, silakan tanya saya via YM..
Simpleks merupakan materi yang cukup membuat pusing di awal pelajaran Riset Operasi, namun materi sesudahnya akan berasa lebih mudah, misalnya masalah penugasan, transportasi, dynamic programming..
Jika materi di atas sudah kalian pahami, maka kalian boleh melanjutkan ke tahap berikutnya.. (Post untuk berikutnya sedang dibuat :P)..
Sumber: Buku Riset Operasi: Suatu Pengantar oleh Hamdy A Taha.
Click Here to Read More..
